Состояние электронов в атомах
Понятие о волновой механике. Теория Бора оказала огромные услуги физике и химии, подойдя, с одной стороны, к раскрытию законов спектроскопии и объяснению механизма лучеиспускания, а с другой — к выяснению структуры отдельных атомов и установлению связи между ними. Однако оставалось еще много явлений в этой области, объяснить которые теория Бора не могла.
Движение электронов в атомах рисовалось Бору до известной степени как простое механическое перемещение, между тем как оно является весьма сложным и своеобразным. Своеобразие движения электронов было раскрыто новой теорией — квантовой, или волновой, механикой.
Эта теория исходит из положения, что законы механики Ньютона, справедливые для тел с достаточно большой массой: (т. е. для таких, с которыми мы обычно встречаемся на практике), неприменимы к движению электронов в атоме и должны быть заменены новыми законами, согласующимися с особенностями этого движения.
Квантовая механика показывает, что законы движения электронов имеют много общего с законами распространения волн, почему она и называется иначе волновой механикой. Так, согласно принципам квантовой механики, при рассеянии электронов кристаллами должны наблюдаться явления диффракции, как и при рассеянии рентгеновых лучей. Диффракция электронов действительно была вскоре обнаружена и в настоящее время применяется для исследования строения вещества столь же широко, как и диффракция рентгеновых лучей. В частности, на диффракции электронов основано устройство электронного микроскопа.
Так как математическая сторона новой теории является очень сложной, то мы не будем на ней останавливаться. Укажем только, что основным уравнением в волновой механике является уравнение, связывающее длину волны λ для потока электронов с их скоростью v и массой т:
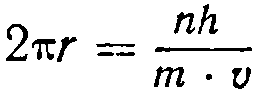
где π — целое число. Это и есть математическое выражение первого постулата Бора, которое он в 1913г. положил в основу расчета движения электрона в атоме водорода.
В приведенном уравнении множитель п, называемый главным квантовым числом, может принимать значение любого целого числа от 1 до бесконечности.
Главное квантовое число определяет уровень энергии, которому отвечает данная орбита, и ее удаленность от ядра. Значение n = 1 соответствует наиболее низкому энергетическому уровню, обозначаемому буквой K; значение π = 2 — энергетическому уровню L и т. д.
Следует заметить, что современная волновая механика в слово «орбита» вкладывает иной смысл, чем тот, который оно имело в теории Бора. Дело в том, что волновая механика рассматривает только большую или меньшую вероятность нахождения быстро движущегося электрона в той или иной точке пространства. Поэтому под словом «орбита» в волновой механике понимают ту область (сферу) вокруг ядра, в которой в среднем чаще всего находится электрон.
Вероятность нахождения электрона может быть выражена также с помощью понятия об электронном облаке. Электрон так быстро движется вокруг ядра, что можно представить себе его электрический заряд «размазанным» в облако отрицательного электричества. Плотность облака больше там, где больше вероятность пребывания электрона.
Таким образом, понятие об электронной орбите как об определенной линии заменяется в волновой механике понятием об электронной сфере или электронном облаке. Так, например, круговой орбите электрона в атоме водорода с главным квантовым числом п = 1 соответствует электронное облако, в котором наибольшая плотность находится вблизи шарового слоя с радиусом r = 0,53 ангстрема, равным радиусу первой боровской орбиты. Однако электрон может находиться и на большем и на меньшем расстоянии от ядра, только вероятность его нахождения здесь будет меньшей. При п = 2 наибольшая плотность электронного облака расположена дальше от ядра и т. д.
Побочное квантовое число l при данном главном квантовом числе п может принимать все значения целых чисел от 0 до n— 1. Так, если главное квантовое число п равно 1, то побочное число l будет равно нулю. В этомслучае электронное облако имеет форму шара (рис. 28, а).
Магнитное квантовое число т определяет положение плоскости орбиты электрона в пространстве или, согласно представлениям волновой механики, то направление, в котором вытянуто электронное облако. Это число может иметь все значения целых чисел как положительные, так и отрицательные,. но только в пределах величины l. Например, при l, равном нулю, т тоже равно

нулю; если l равно трем, то m может быть равным: —3, —2, —1, 0, 1,2, 3.
Однако электрон в атоме вращается не только вокруг ядра, но еще и вокруг собственной оси, причем возможно его вращение в двух противоположных направлениях. Это вращение электрона (так называемый «спин») характеризуется четвертым, спиновым квантовым числом s. Последнее может иметь только два значения — положительное и отрицательное — соответственно двум возможным направлениям вращения электрона.Указанными четырьмя квантовыми числами можно охарактеризовать всю совокупность сложных движений электрона в атоме. Однако они еще не дают исчерпывающего представления о распределении электронов в атоме, так как число их произвольных сочетаний между собой неограниченно велико.На основании анализа спектров и учета положения элементов в периодической системе физиком Паули был найден общий принцип, позволяющий избрать те сочетания квантовых чисел, которые отвечают реальной действительности. Согласно этому принципу, ни в одном атоме нет электронов, сходных во всех отношениях. Иначе говоря, два электрона в атоме не могут иметь четыре одинаковых квантовых числа.
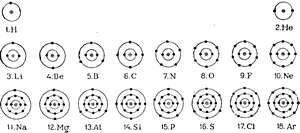
Так, например, первом энергетическом уровне (n=1; l = 0; т = 0) могут находиться только два электрона, отличающиеся своими спинами.На втором энергетическом уровне, отвечающем квантовому числу 2, в состоянии 5, или на s-орбите (l = 0; т = 0), могут быть два электрона с противоположными спинами и в состояниях р, или на р-орбитах (l — 1, m = —1, 0, +1), по два электрона на каждой. Всего, таким образом, на втором энергетическом уровне может находиться восемь электронов (см. табл. 6).При главному квантовом числе n = 3 побочное квантовое число l может принимать значения 0, 1 и 2 (s, р и d),которым соответствуют следующие значения т:при l = 0 т = 0при l=1 т = — 1, 0, + 1приl = 2 т = — 2, — 1, 0, + 1, +2 Так как в каждом состоянии т может быть два электрона, то всего на третьем энергетическом уровне, отвечающем n = 3, могут разместиться 18 электронов (табл. 8 на стр. 162—164). Таким же образом не трудно подсчитать, что на четвертом энергетическом уровне (n = 4) может быть не более 32 электронов. Вообще же максимальное число электронов N, которое может находиться на данном энергетическом уровне п
n, определяется в соответствии с принципом Паули уже известной формулой N = 2n2.Расположение электронов в атомах удобно записывать в виде кратких формул, которые составляются следующим образом. Сначала пишут цифру, указывающую главное квантовое число, за нею следует буква, обозначающая побочное квантовое число, и в виде показателя к ней пишут число электронов, находящихся
| Расположение электронов в атомах | элементов малых | периодов | |||||
| Обозначение слоя | К | L | M | ||||
| Главное квантовое число n | 1 | 2 | 3 | ||||
| Побочное квантовое число l | 0 | 0 | l | 0 | l | 2 | |
| Буквенное обозначение числа l | s | s | P | s | p | d | |
| 1. Водород | н | 1 | |||||
| 2. Гелий | Не | 2 | |||||
| 3. Литий | Li | 2 | 1 | ||||
| 4. Бериллий | Be | 2 | 2 | ||||
| 5. Бор | в | 2 | 2 | 1 | |||
| 6. Углерод | с | 2 | 2 | 2 | |||
| 7. Азот | N | 2 | 2 | 3 | |||
| 8. Кислород | О | 2 | 2 | 4 | |||
| 9. Фтор | F | 2 | 2 | 5 | |||
| 10. Неон | Ne | 2 | 2 | 6 | |||
| 11. Натрий | Na | 2 | 2 | 6 | 1 | ||
| 12. Магний | Mg | 2 | 2 | 6 | 2 | ||
| 13. Алюминий | Al | 2 | 2 | 6 | 2 | 1 | |
| 14. Кремний | Si | 2 | 2 | 6 | 2 | 2 | |
| 15. Фосфор | P | 2 | 2 | 6 | 2 | 3 | |
| 16. Сера | S | 2 | 2 | 6 | 2 | 4 | |
| 17. Хлор | Cl | 2 | 2 | 6 | 2 | 5 | |
| 18. Аргон | Ar | 2 | 2 | 6 | 2 | 6 | |
на соответствующих орбитах. Так, например, «электронная формула» атома водорода будет: 1s1, атома гелия — 1s2, атома лития— 1s2, 2s1, атома кислорода — 1s2, 2s2, 2р4, атома неона — 1s2, 2s2, 2р6, атома алюминия — 1s2, 2s2, 2р6, 3s2, 3р1 и т. д.
Вы читаете, статья на тему Состояние электронов в атомах

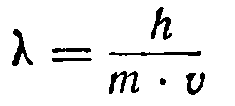
Добавить комментарий
Для отправки комментария вам необходимо авторизоваться.