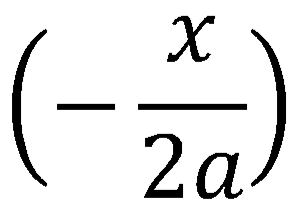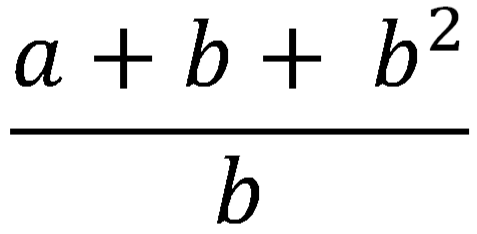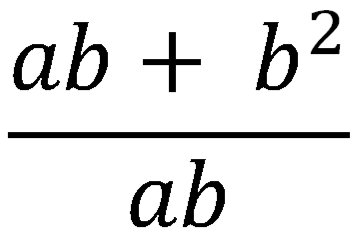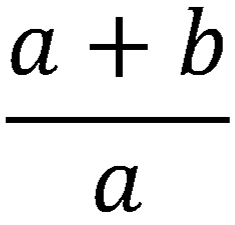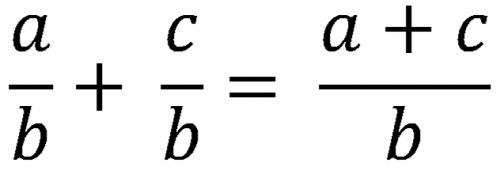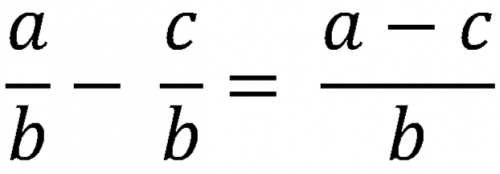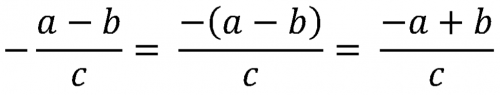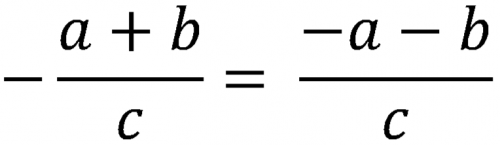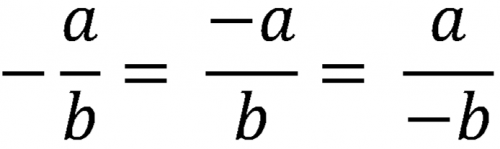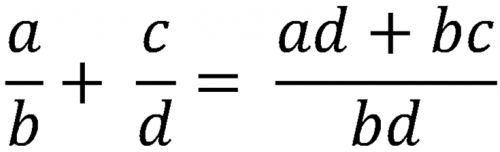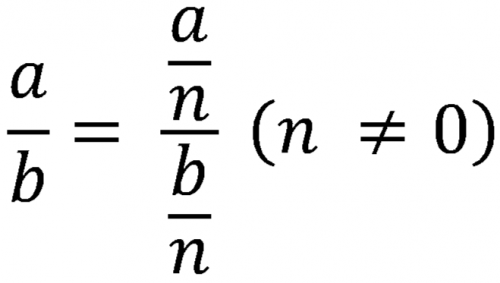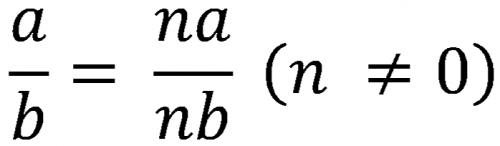Теория:
При сложении или вычитании дробей следует сначала привести их к общему знаменателю, а затем надписать над ним сумму (или разность) числителей.
При вычитании дроби, когда перед ней стоит знак минус, необходимо, до приведения подобных членов, переменить знаки у всех членов числителя.
Знак этот относится ко всей дроби, а не только к числителю или знаменателю; так, например в выражении:
знак минус относиться к дроби, которой и числитель х и знаменатель 2а — положительные.
Чтобы изменить знак числителя или знаменателя, необходимо изменить его у всех членов дроби.
Нельзя сокращать какой-либо член в числителе и знаменателе, если один из них является многочленом.
В выражении:
члены с буквой b в числителе и знаменателе не могут быть сокращены.
Сокращать можно только на множители, входящие во все члены числителя и знаменателя, так как это не изменяет величины дроби.
Так например в выражении:
b являйся общим множителем всех членов числителя и знаменателя, а потому его можно сократить.
Сделав это, получим:
Дроби всегда следует приводить к простейшему виду, при котором числитель и знаменатель не имеют общих множителей.
Для этого разлагают числитель и знаменатель на множители и сокращают те из них, которые являются общими для членов того или другого.
Числитель и знаменатель дроби можно умножить или разделить на одну и ту же величину (неравную нулю), так как величина дроби от этого не изменится.
Практика:
Примеры для решения