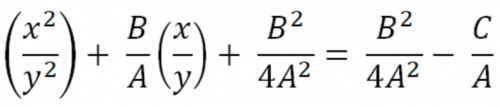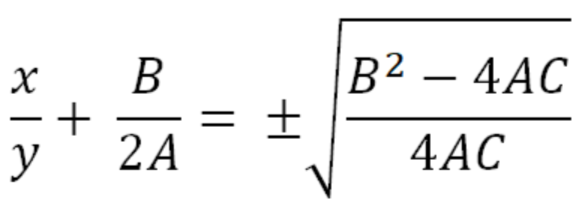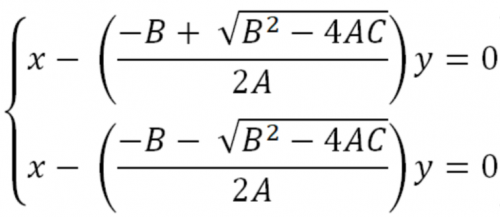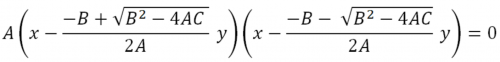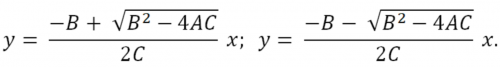Теория:
Однородные квадратные уравнения это уравнения, все члены которых имеют один и тот же порядок (одно и то же измерение) по отношению к содержащимся в них неизвестным.
Общая форма однородного квадратного уравнения такова:
(ур-ние 1) Ах2 + Вху + Cy2 = 0
Уравнения этого вида всегда могут быть разложены на множители.
Деля на Ах2 и дополняя до квадрата, получим:
Извлекая квадратный корень, имеем (ур-ние 2):
Интересно отметить, что отношение неизвестных в ур-нии [2] имеет ту же величину, что и корни уравнения ах2 + bx + c = 0, написанного в явной форме.
Выражение [2] можно представить в таком виде (ур-ние 3):
Теперь линейные уравнения можно получить посредством прямой подстановки значений коэффициентов уравнения [1] в [3].
Уравнение [1] может быть написано в виде произведения двух множителей:
Множители, на которые разлагается трехлен [1], могут быть получены решением ур-ния [1] относительно — Линейные уравнения представляются в виде:
Если одно из двух квадратных уравнений, входящих в систему, однородно, то система решается посредством разложения на множители однородного уравнения.
Практика:
Пример решения однородных квадратных уравнений
Решить систему:
x2 — 3y2 + 2y = 3 (a)
2x2 — 7ху + 6y2 = 0. (б)
Уравнение (б) принадлежит к виду [1], а потому может быть разложено на множители.
Имеем:
А = 2, В = — 7, С = 6.
Подставляя в [3], получим:
x — ((7 + √(49 — 4 • 2 • 6)/(2 • 2)) y = 0 .
x — 2y = 0 или х = 2у.
Кроме того:
x — ((7 -√(49 — 4 • 2 • 6)/(2 • 2))y = 0.
x — (3/2)y = 0 или x = (3/2)y.
Подставляя значение х = 2у и х = (3/2) y уравнение (а), имеем:
x = 2, -6, 2 + √-5, 2 — √ -5.
y = 1, -3, (4 + 2√ -5)/3, (4 — 2√ -5)/3.