Давление газа (пример, измерение)

Давление газа это физическая величина, которая зависит от нескольких факторов: температура, объем и атмосферного давления.

Давление = (число столкновений / секунда)(1/площадь)(импульс / столкновение)

Закон Авогадро позволяет идентифицировать молекулы, присутствующие в газе. На основании этого закона можно объяснить также, почему объемы реагирующих газов находятся в таком же простом отношении, что и числа молей в уравнениях реакций.

Что такое давление газа

Давление — важная характеристика газа. Поэтому возможность объяснения природы давления газа на основании кинетической теории является большим успехом.

Измерение давления газа

Газ оказывает равномерное давление на все стенки сосуда, в который он заключен. Стандартным методом измерения давления является определение высоты столба ртути, уравновешивающего давление газа.

Прибор для измерения давления воздуха показан на рис. , А; он называется барометром. Мы можем сделать барометр сами. Для этого надо наполнить длинную трубку, запаянную с одного конца, ртутью и затем опустить ее открытым концом в сосуд, также наполненный ртутью.

Ртуть из трубки будет стекать в сосуд до тех пор, пока давление столба ртутив трубке не сравняется с давлением воздуха. В приведенном примере давление воздуха равно 755 миллиметрам ртутного столба (755 мм рт ст.).

Эта цифра выражает высоту столба ртути. (Заметим, что в верхней части трубки находятся только пары ртути. При комнатной температуре давление этих паров невелико — приблизительно 10^-3 мм рт. ст.

Измерение давления газа барометром

Давление данного газа можно измерить с помощью прибора, аналогичного барометру; он называется манометром. На рис. , Б и В по казаны манометры двух типов. На рис. , Б изображен U-образный манометр с закрытым концом, в котором давление столба ртути уравновешивается давлением газа, находящегося в колбе.

Давление газа в данном случае равно 105 мм рт. ст. Так же, как и в барометре, в верхней части правого колена трубки находятся лишь пары ртути.

Прибор, показанный на рис., В, отличается от этого манометра тем, что в нем правое колено трубки открыто. В манометре такого типа атмосферное давление направлено на столб ртути в правом колене.

Таким образом, давление в колбе и давление столба ртути суммарно точно равны атмосферному давлению. В приведенном примере давление газа составляет 755—650 = 105 мм рт. ст.; при измерении с помощью манометра с закрытым концом было получено такое же давление.

Нормальные условия температуры и давления. В химических опытах часто надо знать два важнейших условия — температуру и давление. Поэтому во время опыта химики обычно измеряют температуру и давление и поддерживают их на определенном уровне.

Кроме того, многие экспериментальные данные полезно привести к общепринятым нормальным условиям температуры и давления. Это облегчает сравнение различных результатов, полученных разными химическими лабораториями.

Температуру 0°С легко достичь и поддерживать с помощью бани с тающим льдом. Большинство термометров калибруется по этой температуре, что в свою очередь облегчает измерения. Температура, которую легко поддерживать и измерять, является хорошим стандартом температуры.

Давление воздуха в различные дни и в разных местах неодинаково. Тем не менее давление воздуха всегда близко к 760 мм рт. ст. Поэтому атмосферное давление является удобным, хотя и приблизительным, нормальным давлением.

Однако для многих целей это давление недостаточно постоянно. По международному соглашению, нормальным давлением для газов является давление столба ртути высотой 760 мм. Это нормальное давление часто записывают просто как одну атмосферу (1 атм).

Нормальная температура и давлением

Таким образом, химики приняли температуру 0° С и давление 1 атм в качестве удобных нормальных условий. Эти условия — температура 0° С и давление 760 мм рт. ст. — называются нормальными температурой и давлением.

Нормальное давление определяется по показаниям стандартного барометра. В стандартном барометре принимается во внимание то, что гравитационное притяжение ртути Землей мало изменяется в зависимости от места и что при нагревании ртуть расширяется и становится менее плотной.

Так, столб ртути в барометре при 20° С на несколько миллиметров выше, чем при 0° С. В стандартном барометре ртуть находится при 0° С. По опубликованным таблицам можно рассчитать, насколько различаются показания обычного и стандартного барометров.

Поправка редко превышает 1—2 мм рт. ст. и часто пренебрежимо мала по сравнению с другими возможными ошибками. Если другие ваши измерения недостаточно точны, не следует вносить поправку в показания обычного барометра.

Причина возникновения давления газа

Газ оказывает давление в результате столкновения его частиц со стенками сосуда. Такая модель давления газа составляет часть кинетической теории. Каждый раз, когда молекула газа сталкивается со стенкой (или с поверхностью ртути), она оказывает на стенку небольшое давление, подобно тому как давит на стену брошенный в нее мяч.

Действующая на единицу поверхности сила, называемая давлением, прямо пропорциональна числу молекул, сталкивающихся с единицей площади поверхности.

Если в данном объеме содержится вдвое больше молекул, то число столкновений на единицу поверхности также увеличится вдвое и, следовательно, давление возрастет в 2 раза по сравнению с первоначальным.

Именно этим объясняется увеличение давления в автомобильной шине, когда в нее накачивается воздух. Если объем и температура шины не изменяются, то давление возрастает прямо пропорционально числу молей накачиваемого воздуха.

Упражнение для самообразования

Сосуд определенного объема содержит 2 моля газа при комнатной температуре. Давление в сосуде — 4 атм. В сосуд вводят еще 3 моля газа при той же температуре.

На основании приведенных выше рассуждений покажите, что теперь давление равно 10 атм.

Парциальное давление

Парциальное давление — это такое давление, которое оказывал бы газ, если бы в сосуде находился он один.

На рисунке изображены три колбы емкостью 1 л при 25° С. В первой колбе содержится 0,0050 моля воздуха. Манометр показывает, что давление равно 93 мм рт. ст.

Во второй колбе находится 0,0011 моля паров воды. Давление в этой колбе равно 20 мм рт. ст. В третьей колбе содержится смесь 0,0050 моля воздуха и 0,0011 моля паров воды.

Третий манометр показывает, что давление в этой колбе равно 113 мм рт. ст.

Этот опыт показывает, что давление смеси газов точно равно сумме давления воздуха и давления паров воды:

113 мм рт. ст. = 93 мм рт. ст. + 20 мм рт. ст. (4)

Общее давление можно рассматривать как сумму давлений, создаваемых каждым компонентом смеси. 

Давление, оказываемое каждым газом газовой смеси, называется парциальным давлением этого газа.

В примере, приведенном на рис. 2 -3, общее давление в третьей колбе равно 113 мм рт. ст. Парциальное давление паров воды равно 20 мм рт. ст., парциальное давление воздуха — 93 мм рт. ст.

Упражнение для самообразования

Предположим, что в 0,0050 моля воздуха содержится 0,0040 моля азота N₂ и 0,0010 моля кислорода О₂. Каково парциальное давление кислорода в первой колбе, показанной на рис. 2-3? Каково парциальное давление кислорода в третьей колбе?

Результаты опыта, иллюстрированного рис. 2-3, легко объяснить с помощью кинетической теории газов.

Молекулы газа находятся на таком большом расстоянии друг от друга, что каждая из них ведет себя независимо, внося свою долю в общее давление в результате столкновений со стенками сосуда Молекулы воды в третьей колбе редко сталкиваются друг с другом или с молекулами воздуха.

Поэтому они оказывают точно такое же давление, как и во второй колбе, — давление, которое существовало бы в третьей колбе в отсутствие воздуха.

Давление, создаваемое 0,0011 моля паров воды, будет равно 20 мм рт. ст. независимо от того, имеется ли в колбе воздух. 0,0050 моля воздуха создают давление 93 мм рт, ст. независимо от того, имеются ли в колбе пары воды.

Сумма парциальных давлений 93 и 20 мм рт. ст. определяет общее давление в колбе.

Температура и кинетическая энергия

Если кинетическая теория применима к газам, то можно ожидать, что давление зависит не только от числа молей в единице объема. Например, масса молекул и скорость их движения также имеют большое значение.

Как известно, волейбольный мяч ударяется в руку игрока с большей силой, чем мяч для настольного тенниса, летящий с той же скоростью. Быстро летящий мяч ударяет сильнее, чем мяч, летящий медленно.

Для того чтобы выяснить, какое значение в кинетической теории имеют масса и скорость молекул, рассмотрим понятие о температуре.

Чтобы измерить температуру газа, мы погружаем в него термометр. Если термометр холоднее, чем система, то определенное количество тепла передается термометру до тех пор, пока газ и термометр не будут иметь одинаковую температуру.

При этом термометр показывает числовое значение температуры. Если термометр нагрет сильнее, чем газ, то определенное количество тепла передается от него системе Если же передачи тепла не происходит, то говорят, что термометр находится в тепловом равновесии с газом.

Типы термометров

Существует несколько типов термометров. В термометрах можно использовать любое вещество, которое обладает легко измеряемым свойством, чувствительным к изменению температуры. Действие обычного ртутного термометра основано на том, что при повышении температуры жидкость расширяется.

Объем твердых веществ и газов также изменяется в зависимости от температуры. Поэтому и эти вещества можно использовать в термометрах. Если газ поддерживать при постоянном объеме, то с увеличением температуры возрастает давление.

Такой метод наиболее часто используется для измерения температуры: объем газа поддерживают постоянным, при этом давление изменяется в зависимости от температуры.

Измерение температуры газа термометром

Измерим температуру газа А, приведя его в контакт с газом Б (наш термометр). Если эти два газа в начальный момент имеют различные температуры, то произойдет передача тепла.

Тепло от более нагретого газа будет передаваться менее нагретому. Когда передача тепла прекратится, газы достигнут теплового равновесия. Теперь оба газа имеют одинаковую температуру.

То, что при этом происходит, можно представить с помощью кинетической теории газов. Предположим, что температура газа А выше, чем газа Б. Мы объясняем тем, что молекулы газа А обладают большей энергией движения по сравнению с энергией движения молекул газа Б — молекулы газа А имеют более высокую кинетическую энергию (в среднем).

Когда газы соприкасаются, быстро движущиеся молекулы газа А при соударении могут передавать кинетическую энергию медленно движущимся молекулам Б. В результате этого переноса кинетической энергии от газа А к газу Б повышается температура газа Б и понижается температура газа А.

Когда переход кинетической энергии от одного газа к другому в результате теплового контакта между молекулами газов А и Б заканчивается, эти газы находятся в тепловом равновесии; они имеют одинаковую температуру.

Таким образом, теплообмен между двумя газами мы представляем как переход кинетической энергии. Этот процесс длится до тех пор, пока молекулы обоих газов не приобретут одинаковую среднюю кинетическую энергию.

Результатом этого является достижение обоими газами одинаковой температуры. Это и есть основная предпосылка кинетической теории: если газы находятся при одной и той же температуре, их молекулы имеют одинаковую среднюю кинетическую энергию.

Абсолютная температура

Количественные соотношения между температурой и объемом газов впервые изучал французский ученый Жак Шарль в 1787 г. Он нашел, что первоначальные объемы всех газов при их нагревании в одном и том же интервале температур увеличиваются в одинаковой степени.

(В этих опытах давление сохранялось постоянным.) Эти соотношения выводятся на основании простого опыта. В узкую стеклянную трубку длиной 0,5 м, запаянную с одного конца, помещают каплю ртути.

Эта капля удерживается воздухом на некоторой высоте. Поскольку трубка имеет равномерное сечение, мы можем принять высоту слоя воздуха до капли ртути за меру его объема.

Ртутная пробка может перемещаться вверх или вниз, благодаря чему в трубке сохраняется постоянное давление.

Мы можем поместить трубку в ледяную воду (0° С) и измерить относительный объем воздуха. Если трубку перенести в кипящую воду (100° С при 1 атм), то относительный объем увеличится.

По результатам этих измерений и результатам аналогичных измерений, полученным для других температур, можно составить приведенную ниже таблицу 1.

Таблица 1
Температура, °С	Относительный объем (измеренный по высоте слоя воздуха)
200	1,73
100	1,37
50	1,18
0	1,00

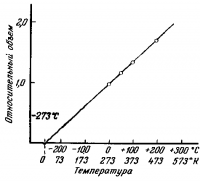
Если мы отложим значения относительного объема на оси ординат (вертикальная ось), а температуру на оси абсцисс (горизонтальная ось), то получим график, изображенный на рис. 3.

Через экспериментальные точки проходит прямая линия. Если продолжить прямую линию вверх, то можно видеть, что объем воздуха при 273° С вдвое больше, чем при 0° С.

Если продолжить эту линию вниз, то получается, что объем становится равным нулю при.—273°С. Изменение объема при изменении температуры на 1°С составляет 1/273 объема при 0° С. В действительности все газы сжижаются еще до того, как их температура достигнет —273° С.

Если газ нагревать или охлаждать при постоянном объеме, то его давление тоже изменяется на 1/273 давления при 0° С. Давление газа становится равным нулю при —273° С. Согласно кинетической теории, при этой температуре движение молекул прекращается. Кинетическая энергия становится равной нулю.

Абсолютная шкала температур

Абсолютная шкала температур обладает тем преимуществом, что ее нуль соответствует —273° С. В то время как «нуль» стоградусной шкалы выбран произвольно (температура плавления льда), нулевая точка абсолютной шкалы имеет определенный смысл в кинетической теории.

Если мы выражаем температуры в абсолютных градусах, то при этом объем определенного количества газа (при постоянном давлении) прямо пропорционален температуре.

В соответствии с кинетической теорией кинетическая энергия молекул прямо пропорциональна абсолютной температуре. По этой причине мы часто выражаем температуру по абсолютной шкале.

Эта шкала температур, имеющая такую же единицу измерения (градус), что и стоградусная шкала, называется шкалой Кельвина.

Температура по этой шкале выражается в градусах Кельвина (° К). На рис. 4-5 приведены значения температуры, выраженные в градусах Кельвина и по стоградусной шкале — в градусах Цельсия.

Все числовые значения по шкале Кельвина на 273 градуса выше, чем соответствующие температуры, выраженные в градусах Цельсия.

Упражнение для самообразования

а) Выразите следующие температуры в градусах Кельвина:

Температура кипения воды 100°С Температура замерзания ртути 38,9°С Температура кипения жидкого, азота —196°С

б) Выразите следующие температуры в градусах Цельсия:

Температура плавления свинца 600 °К Комнатная температура 298 °К Температура кипения жидкого гелия 4°К.

2) При реакции 2,0 • 10^-3 моля металлического магния Mg с соляной кислотой НСl выделяется газообразный водород, который при 25° С и давлении 1 атм занимает объем 49,0 мл.

а) При реакции 1 моля магния с соляной кислотой выделяется 1 моль водорода. Вычислите объем 1 моля водорода при 25° С (298° К) и давлении 1 атм.

б) Вычислите объем 1 моля водорода при 0° С (273° К) и давлении 1 атм.

Как указывалось выше, при температуре 0° К всякое движение молекул прекращается. Кинетическая энергия становится равной нулю.

При температурах, близких к 0° К, наблюдаются очень интересные явления (например, сверхпроводимость многих металлов и сверхтекучесть жидкого гелия). В связи с этим ученые весьма заинтересованы в достижении температур, как можно более близких к абсолютному нулю.

Для охлаждения очень часто используют жидкий водород (кипящий при 20° К) и жидкий гелий (кипящий при 4° К). При пониженном давлении гелий кипит при еще более низкой температуре, и это обеспечивает достижение температур, близких к 1° К.

Разработаны другие более сложные методы, с помощью которых может быть достигнута температура до 0,001° К. Однако в этих условиях термометрия становится такой же трудной, как и сам метод достижения низких температур.

Закон Авогадро и кинетическая теория

Кинетическая теория основана на предположении, что если два газа находятся при одной и той же температуре, то молекулы этих газов имеют одинаковую среднюю кинетическую энергию.

То, что с помощью этой теории можно объяснить закон Авогадро, является одним из наиболее важных ее успехов.

Мы можем представить закон Авогадро в такой форме: если два газа при одной и той же температуре имеют одинаковое число частиц в данном объеме, то они должны оказывать одинаковое давление. Масса молекулы, а также скорость ее движения должны влиять на давление.

Если молекулы двух газов имеют различные массы, то у них должны быть и разные скорости, чтобы кинетическая энергия оставалась постоянной. Более легкие молекулы должны двигаться быстрее, поэтому они будут сталкиваться со стенками сосуда за 1 сек большее число раз.

Более частые столкновения се стенками сосуда молекул с меньшей массой как раз и компенсируют более слабый «удар» этих молекул при каждом столкновении.

Все это очень хорошо согласуется с законом Авогадро: два газа, занимающие одинаковый объем и находящиеся при одной и той же температуре, оказывают на стенки сосуда одинаковое давление, несмотря на то что массы их молекул различны.

Объяснение закона Авогадро

Закон Авогадро легко можно доказать. Кинетическая энергия движущейся частицы выражается уравнением

КЭ = 1/2 mυ² (5)

где т — масса частицы; υ — скорость движения частицы. Таким образом, для газов А и Б с одинаковой температурой мы имеем

(КЭ)_А = (КЭ)_Б (6)

или

m_Аυ²_А=^т_Бυ²Б (7)

Теперь предположим, что мы поместили п молекул в кубический сосуд со стороной d. Давление определяется числом столкновений молекул со стенками в 1 сек на 1 см², умноженным на импульс, передаваемый за одно столкновение:

Давление = (число столкновений / секунда)(1/площадь)(импульс / столкновение)

Импульс зависит от массы и скорости частицы. Частица приближается к стенке с импульсом mv и после удара отскакивает от нее с тем же по величине импульсом, но с противоположным знаком. Поэтому импульс, переданный стенке, равен

Импульс = 2mυ (9)

С другой стороны, число столкновений со стенкой в 1 сек зависит от размеров сосуда и скорости частицы (так как молекула отскакивает от одной стенки к другой и обратно). Мы можем предположить, что треть молекул движется взад и вперед в данном направлении между двумя противоположными стенками.

Поэтому если в сосуде находится п молекул, то п/3 молекул ударяются в эти две стенки. Столкновение с одной из стенок происходит тогда, когда молекула пройдет расстояние между стенками d и обратно, т. е. общий путь равен 2d.

Число столкновений/секунда = число частиц в обоих направлениях/время за которое проходит путь 2d

Число столкновений/секунда = (n/3)/(2d/υ) = (n/3)(υ/2d) = nυ/6d (10)

Комбинируя уравнение находим, что

Давление = (Число столкновений/секунда)(1/Площадь)(Импульс/столкновение) = (1nυ/6d)(1/d²)2mυ = 1/3(n/d³)(mυ²) (11)

Применив уравнение к каждому из двух газов получим

P_A = 1/3(n_A/d³)(m_Aυ²_A) (12)

P_Б = 1/3(n_Б/d³)(m_Бυ²_Б) (13)

Если газы имеют одинаковое давление (Р_А= Р_Б), мы можем приравнять уравнения (12) и (13):

1/3(n_A/d³)(m_Aυ²_A) = P_Б = 1/3(n_Б/d³)(m_Бυ²_Б) (14)

Если температура обоих газов одинакова, то справедливо уравнение (7). Тогда уравнение (14) принимает вид

n_A/d³ = n_Бd³

Таким образом, мы видим, что при одинаковых температуре и давлении два газа имеют равное число молекул в единице объема. А это и есть закон Авогадро.

Идеальный газ

Это газ, который ведет себя так, как будто между его молекулами не существует никакого взаимодействия, называется идеальным газом.

Экспериментальные данные о давлении и объеме для кислорода, аммиака и хлористого водорода. В каждом случае в пределах ошибки опыта наблюдается определенная закономерность: PV = const.

Многочисленные опыты подтвердили, что большинство газов подчиняется этой простой закономерности. Из этого общего правила есть и исключения, как и в случае других научных утверждений.

Любое правило выводится на основании ряда измерений, каждое из которых допускает некоторую неточность, поэтому постоянство PV установлено только в определенных пределах ошибки. Более того, существуют пределы давления, в которых можно изучать поведение газов.

Пример идеального газа

Например, рассмотрим данные для 17,0 г аммиака при 0° С, . По этим данным PV = 24,5, но для этой величины должны быть учтены ошибки измерения и пределы применимости этих данных. В этом случае ошибка равна ±0,7, а пределы давления составляют 0,2—2 атм.

На основании этих данных можно сделать вывод, что произведение объема и давления — постоянная величина, выраженная четырьмя цифрами: PV = 24,50. Однако нельзя сказать с полной уверенностью, что это произведение будет постоянным за пределами 0,2—2 атм, установленными для давления.

Напомним, что правило справедливо лишь в тех пределах, в которых проводились опыты. Если требуется более высокая точность измерений давления и объема при более высоком давлении, то необходимо проводить дополнительные опыты. В приведены результаты таких более точных измерений давления и объема.

Наиболее поразительным в табл. 2 является значительное отклонение от PV = 24,5, наблюдаемое при давлении выше 9,800 атм. Соотношение PV = const больше не соблюдается. Это показывает, насколько осторожно нужно производить экстраполяцию полученных данных за установленные пределы.

Даже при более низком давлении, чем давление, при котором происходит конденсация, произведение давления и объема не совсем постоянно.

Проводя измерения с достаточной тщательностью и точностью, мы убеждаемся, что произведение PV для аммиака при 25° С не является постоянным. Оно изменяется от 24,45 при 0,1000 атм до 23,10 при 9,800 атм, когда уже начинается конденсация.

Подобные измерения с 28,0 г окиси углерода при 0° С показывают, что произведение PV равно 22,410 при 0,2500 апгм, но при давлении 4,000 атм это произведение становится равным 22,308. Такой тип отклонения от постоянной величины является общим для всех газов.

В результате тщательных измерений установлено, что ни для одного газа не соблюдается идеально соотношение PV = const при всех давлениях. С другой стороны, все газы подчиняются этому правилу приблизительно, и соответствие улучшается при уменьшении давления.

Таким образом, мы нашли, что при понижении давления каждый газ приближается к идеальному газу, для которого PV = const.

Объяснение образования идеального газа

Для отклонения от правила имеется разумное объяснение. Кинетическая теория, «объясняющая» поведение газа, основана на предположении, что между частицами газа не существует взаимодействия. Но реальные молекулы взаимодействуют друг с другом!

Конденсация любого газа при охлаждении показывает, что между частицами действуют силы притяжения. Эти силы не имеют существенного значения, когда молекулы находятся далеко друг от друга (т. е. при низких давлениях), но они становятся заметными при более высоких давлениях.

Теперь мы убедились, что кинетическая теория справедлива для «идеализированного» газа, т. е. для газа, в котором отсутствует взаимодействие между молекулами.

Каждый реальный газ приближается к такому идеальному поведению при достаточно низком давлении. В этих условиях молекулы в среднем настолько удалены друг от друга, что силы притяжения незначительны.

Давление и объем аммиака

Результаты точных измерений давления и объема для 17.0 г аммиака при 25°С Таблица 2

Давление, атм	Объем, л	PV
0,1000	244,5	24,45
0,2000	122,2	24,44
0,4000	61,02	24,41
0,8000	30,44	24,35
2,000	12,17	24,34
4,000	5,975	23,90
8,000	2,925	23,40
9,800	2,360	23,10а
9,800	0,020	0,20б
20,00	0,020	0,40в
50,00	0,020	1,0в

^а Начинается конденсация.

^б Газа не остается, только жидкость.

^в Жидкость.

Молярные объемы газов

Молярные объемы некоторых газов при температуре 0°С и давлении 1 атм Таблица 3

Газ	Формула	Молекулярный вес, г	Молярный объем, л
Водород	Н2	2,0160	22,430
Гелий	Не	4,003	22,426
(«Идеальный» газ)	—	—	(22,414)
Азот	N2	28,016	22,402
Окись углерода	СО	28,011	22,402
Кислород	О2	32,000	22,393
Метан	CH4	16,043	22,360
Двуокись углерода	СО2	44,011	22,262
Хлористый водород	HCl	36,465	22,248
Аммиак	NH3	17,032	22,094
Хлор	Сl2	70,914	22,063
Двуокись серы	SO2	64,066	21,888

Закон Авогадро согласуется с кинетической теорией. Следовательно, идеальный газ подчиняется закону Авогадро. При 0° С и давлении 1 апгм 1 моль (6,02•10²³ молекул) идеального газа занимает объем 22,414 л.

Насколько близко реальные газы приближаются к идеальному газу при 0° С и 1 атм, показывают измерения молярного объема — объема, занимаемого 1 молем этого газа. В табл. 3 приведены молярные объемы некоторых газов.

Реальные газы при 0° С и 1 атм близки к идеальному газу (до трех значащих цифр). Каждый газ становится идеальным при уменьшении давления до нуля.

Давление газа вывод

Закономерности, наблюдаемые в поведении газов, в значительной мере помогают понять структуру вещества. Одной из наиболее важных закономерностей является гипотеза Авогадро: одинаковые объемы газов содержат равное число частиц (при одинаковых температуре и давлении).

Эта зависимость используется при определении молекулярных формул веществ, которые необходимо знать для того, чтобы понять природу химической связи.

Согласно кинетической теории, если два газа находятся при одинаковой температуре, то молекулы этих газов обладают одинаковой средней кинетической энергией.

При изменении температуры газа при постоянном давлении объем прямо пропорционален температуре, если температура выражена в градусах абсолютной шкалы.

Температура плавления льда (0° С) по этой шкале (называемой шкалой Кельвина) равна 273° К. Температура кипения воды при 1 атм (100° С) равна 373° К- Предполагается, что при температуре, равной нулю по шкале Кельвина, прекращается всякое движение молекул.

Все эти данные подтверждают  в справедливость атомно-молекулярной теории и способствуют ее дальнейшему развитию.

Предположения, принятые при рассмотрении газов, применимы также и в случае конденсированных фаз — жидкостей и твердых веществ.

Вопросы и задачи для самообразования

1. Сколько молекул содержится в молярном объеме газа при 100° С? При 0°С?

2. Определите молярный объем воды в каждом из следующих случаев:

а) Твердое вещество, 0° С; плотность льда 0,915 г/см³.

б) Жидкость, 0° С; плотность воды (жидкость, 0°С) 1,000 г/см³.

в) Газ, 100° С; плотность паров воды (100° С, 1 атм) 5,88•10^-4 г/см³.

3. Каков молекулярный вес газа, если при 0° С и 1 атм 1,00 л газа весит 2,00 г?

4. При реакции двуокиси серы с кислородом образуется трехокись серы:

2SO₂ (г) + O₂ (г) →2SO₃ (г)

5. Стеклянная колба после удаления из нее воздуха весит 108,11 г. Наполненная кислородом при комнатной температуре и давлении 1 атм колба весит 109,56 г. Если эту колбу наполнить вулканическим газом при таких же условиях, то она будет весить 111,01 г. Какая из указанных формул для вулканического газа соответствует приведенным данным:

(CO₂, OCS, Si₂H₆, SO₂) (NF₃, SO₃, S₈, CO₂ + Kr).

6. Сжатый газообразный кислород находится в стальном баллоне емкостью 40 л при давлении 130 атм.

а) Сколько молей кислорода содержится в полном баллоне?

б) Сколько это составляет килограммов?

В огнетушителе емкостью 3 л находится 4,4 кг двуокиси углерода. Какой объем будет занимать это количество газа при нормальных условиях?

8. Для наполнения метеорологических зондов часто применяют водород, полученный при реакции гидрида кальция СаН₂ с водой. При этом образуются гидроокись кальция и газообразный водород.

а) Напишите уравнение реакции и определите, сколько молей СаН₂ потребуется для наполнения водородом зонда емкостью 250 л при нормальных условиях температуры и давления.

б) Сколько расходуется воды для получения такого количества водорода?