Соединения в математике представляют собой упражнения и концепции, связанные с объединением различных множеств или структур.
Они играют важную роль в теории множеств, комбинаторике и алгебраической геометрии.
Основное понятие соединений связано с операцией объединения, пересечения и разности между множествами, что позволяет математическим структурам взаимодействовать и формировать новые объекты.
Соединения в математике или операция соединения
Если для изготовления какой-нибудь вещи требуется произвести два действия, причем первое может быть выполнено только одним способом.
А второе r способами, то указанную вещь можно изготовить, сочетая первое действие с любым из r возможных способов осуществления второго действия.
Таким образом данную вещь можно сделать r способами.
Пусть в предыдущем примере первое действие можно осуществить уже не одним, а двумя способами, второе же по-прежнему r способами.
Тогда каждый из двух способов выполнения первого действия можно сочетать с любым из r способов для второго действия, следовательно вещь может быть изготовлена 2r различными способами.
Положим, для изготовления предмета нужно выполнить три действия, причем для первого существует n способов осуществления его, для второго — r и для третьего — s способов.
Рассуждая подобно предыдущему, найдем, что всего возможно n • r • s способов для того, чтобы изготовить данный предмет.
Точно таким же образом, если на должность директора предприятия могут быть приглашены 4 человека, а на должность его помощника 6 человек, то существует 6 X 4 = 24 способа замещения указанных вакансий.
n различных вещей можно раздать х мужчинам и а женщинам (x + a)n способами, так как первую вещь можно раздать (x + a) способами, вторую — также (х + а) способами и т. д.
Следовательно, для n вещей существует:
(х + a) (х + a) (х + a) . . . или (х + a)n
способов распределения.
Всякое расположение предметов, отличающееся порядком их расположения, или самими предметами, называется размещением.
Перестановкой, называются размещения, отличающиеся только порядком расположения предметов, а не самими предметами.
Всякое распределение предметов в группы независимо от порядка, в котором они расположены в этих группах, называется сочетанием.
Например:
аb, ас, ba, bc, са, cb.
ab и bа суть различные перестановки в одном и том же сочетании.
Если рассматривать все три буквы, взятые вместе, то получим 6 перестановок, а именно:
abc, acb, bca, bac, cab, cba,
нo только одно сочетание: abc.
Число размещений n различных предметов
Число размещений n различных предметов, взятых одновременно, равно произведению
n(n — 1)(n — 2)(n — 3)… 3 • 2 • 1 или n!
Предположим, что у нас имеется n различных вещей и мы хотим знать, сколькими способами можно расставить их по n местам.
Можно поставить любую из вещей на первое место, любую из оставшихся n —1 вещей на второе место.
Первые два места могут быть заняты n(n — 1) различными способами.
Продолжая действие в том же порядке, найдем, что последние два места можно заполнить только двумя способами, а последнее лишь одним.
Число размещений n вещей
Число размещений n вещей, взятых по r за-раз, будет равно:
Пусть имеется ряд из r стульев и мы желаем знать, сколькими способами можно рассадить на них r из n человек.
Каждого из людей можно посадить на первый стул. После того как он будет занят, можно занять второй стул любым из (n — 1) оставшихся людей.
Таким образом число возможных размещений на двух стульях равно n(n — 1), если r ≤ n.
Последний r-ый стул можно занять столькими способами, сколько осталось стоящих людей.
Следовательно, если мы захотим выбрать человека, могущего занять r-ый стул, имея уже (r — 1) сидящих, то найдется n — (r -1) или (n — r + 1) людей, не имеющих места.
Общее количество способов рассадить r людей из n на r стульях будет:
n(n — 1)(n — 2)(n — 3) . . . (n — r + 1) = (n(n — 1)(n — 2) . . . 3 • 2 • 1))/((n — r)(n — r — 1) . . . 3 • 2 • 1)) = n!/((n — r)!)
Условились обозначать число размещений из n предметов но r символом:
Число сочетаний из n различных вещей
Число сочетаний из n различных вещей по r одновременно равно:
В предыдущем случае имелось r людей и r! перестановок из них, но только одно сочетание.
Таким образом там было в r! раз больше перестановок, чем сочетаний.
Если число сочетаний равно х, то х • r! есть число возможных размещений:
или


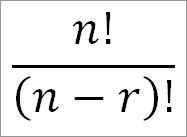
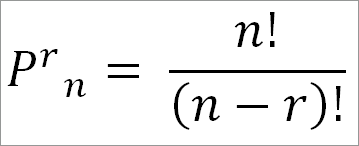
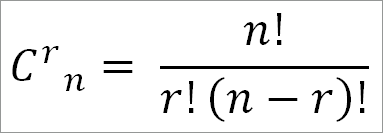
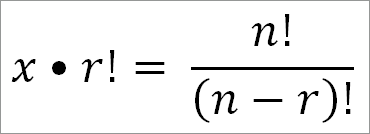
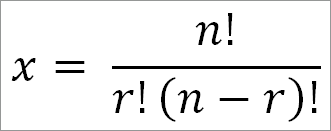
Добавить комментарий
Для отправки комментария вам необходимо авторизоваться.