Неопределенные коэффициенты
Коэффициенты, величины которых в начале решения задачи неизвестны, но определяются впоследствии, называются неопределенными коэффициентами.
Если, например, мы хотим разложить выражение (x — 1)(х + 1)(х — 2), не производя самого перемножения, то можем вообще написать:
(х — 1)(х + 1)(х — 2) = х3 + Aх2 + Вх + С. (1)
С целью определения коэффициентов А, В к С из тождества, которое должно оставаться справедливым для всех значений х, положим в (1) х = 0. В этом случае С = 2.
Если х = 1, то выражение (1) примет вид:
0 = 1 + A + В + С
Если х = —1, то из (1) будем иметь
0 = -1 + A — B + C.
Решая совместно два последние условные уравнения имеем:
А = — 2, В = — 1, С = 2.
Следовательно:
(х — 1)(х + 1)(х — 2) = х3 — 2х2 — х + 2.
Разложение дробей
Пример № 1.
Разложить дробь:
(1 + 2x)/(1 + x + x2)
Первый член разложения получается посредством обыкновенного деления и равен, очевидно, 1 : 1, т. е. 1.
Так как число не делится нацело на знаменателя, то результатом деления явится бесконечный ряд, начинающийся членом 1.
Последующие члены представляют собой выражения с возрастающими степенями х.
Для определения коэффициентов при этих степенях положим:
Это равенство будет справедливо для всех значений х, которые обращают ряд в сходящийся.
Умножая все члены ряда на знаменатель и упрощая его, получим:
Применяя принцип неопределенных коэффициентов, можно приравнять коэффициенты в этих двух рядах.
Совокупность членов, стоящих по левую сторону от знака равенства, можно рассматривать как бесконечный ряд:
1 + 2х + 0х2 + 0х3 + 0х4 + …
Сумма членов этого ряда имеет определенную величину для любых значений х.
В то время как ряд, стоящий по правую сторону знака равенства, имеет определенную величину суммы лишь для тех значений х, которые делают этот ряд (1) сходящимся.
Так как равенство (2) имеет смысл для значений х, обращающих ряд в сходящийся.
То неопределенные величины А, В, С можно определить сравнением коэффициентов при одинаковых степенях х в обеих частях равенства.
Следовательно:
А + 1 = 2; В + А + 1 = 0; С + В + А = 0; D + C + B = 0
и
A = 1; B = -2; C = +1; D = + 1.
Таким образом дробь:
(1 + 2x)/(1 + x + x2) = 1 + x — 2x2 + x3 + x4 + …
Разложение может быть также получено делением.
Пример № 2.
Разложить дробь:
Так как первый член разложения есть очевидно 2/х2 или 2х-2, то полагаем, что дробь после разложения принимает вид:
(2 — x + 2x2)/(x2 — 2x3) = Ax-2 + Bx-1 + C + Dx + Ex2 + …
Освобождая от знаменателя в умножая обе части на x2, имеем:
Сравнивая коэффициенты при одинаковых степенях х и решая уравнения, найдем:
А = 2, В = 3, С = 8, D = 16, E = 32,
откуда
(2 — x + 2x2)/(x2 — 2x3) = 2x-2 + 3x-1 + 8+ 16x + 32x2 + …
Разложение иррациональных выражений
Чтобы разложить выражение √(a + x) методу неопределенных коэффициентов, положим:
√(a + x) = A + Bx + Cx2 + Dx3 + Ex4 + . . .
Возвышая обе стороны в квадрат, найдем:
Сравнивая коэффициенты при одинаковых степенях х, находим:
А2 = а, откуда А = √a
2АВ = 1, ,, B = 1/2A = √a/2a
B2 + 2AC = 0, ,, C = — (√a/8a2)
2AD + 2BC = 0, ,, D = √a/16a3
и наконец,
С2 + 2AE +2BD = 0,
следовательно
E = — (5√a/128a4)
Таким образом
√(a + x) = √a(1 + (x/2a) — (x2/8a2) + (x3/16a3) — (5x4/128a4) + …)
Заданное иррациональное выражение может быть также разложено посредством извлечения корня или по формуле бинома.
Следует, однако, заметить, что, независимо от примененного способа, полученный ряд будет равен данному иррациональному выражению только пои тех значениях х, которые делают ряд сходящимся.
Простейшие дроби
При сложении дробей получается одна дробь, у которой знаменатель равен наименьшему кратному знаменателей слагаемых.
Например,
Часто бывает необходимо произвести обратное действие, а именно разбить данную дробь на сумму или разность дробей, имеющих знаменатель более низкой степени и более удобного вида.
Здесь мы будем рассматривать только такие дроби, у которых числитель имеет более низкую степень, чем знаменатель.
В противном случае, произведя деление, получим целый многочлен и правильную дробь указанного типа.
Число простейших дробей, на которые разлагается данная, зависит от числа простых множителей, на которые можно разложить ее знаменатель.
Рассмотрим следующие случаи разложения:
- Знаменатель разлагается на множители первой степени.
- Знаменатель разлагается на действительные линейные множители.
- Знаменатель содержит множители второе степени, которые не повторяются и не могут быть разложены на линейные.
- Знаменатель содержит одинаковые множители второй степени.
Случай № 1
Знаменатель разлагается на множители первой степени (линейные), которые являются действительными, но различными.
Рассмотрим дробь:
Положим:
(x + 4)/((x — 1)(x — 2)(x — 3)) = (A/(x — 1)) + (B/(x — 2)) + (C/(x — 3))
Умножая обе части равенства на (х — 1)(х — 2)(х — 3), получим:
х + 4 = A(х — 2)(х — 3) + В(х — 1)(х — 3) + С(х — 1(х — 2) = (A + В + С)x2 — (5A + 4В+3С)х + 6A + 3B + 2С.
Сравнивая коэффициенты при одинаковых степенях х, имеем:
0 = A + B + C,
-1 = 5A + 4B + 3C,
4 = 6A + 3B + 2C.
Решая уравнения совместно, находим:
A = 5/2, B = -6, C = 7/2.
Составим теперь уравнение:
(x + 4)/((x — 1)(x — 2)(x — 3)) = (5/(2(x — 1)) — (6/(x — 2)) + (7/(2(x — 3))
Другой способ разложения состоит в рассмотрении отдельных множителей знаменателя, а именно, (х — 1), (х — 2) и (х — 3), а затем в подстановке корней х = 1, 2 и 3 вместо х.
Остаток во всех случаях будет равен нулю.
В этом случае после упрощений будем иметь
х + 4 = А(х — 2)(х — 3) + В(х — 1)(х — 3) + С(х — 1)(х — 2).
Подставим значение корня х = 1:
5 = 2A + 0 + 0, откуда, как и ранее,
A = 5/2
Подставляя корень х = 2, имеем
6 = 0 — B + 0, т. е.
В = -6.
Наконец, принимая х = 3, получим:
7 = 0 + 0 + 2C
C = 7/2 как и раньше.
Правило таково, что множителям (х — а) соответствует простая дробь вида:
A/(x — a)
Случаи № 2
Знаменатель разлагается на действительные линейные множители, некоторые из которых повторяются, как например в дроби:
В этом случае знаменателями отдельных дробей будут не только (х — 1)3, но также (х — 1)3 и (х — 1).
В случае, если они не входят в состав дроби, числители равны нулю.
Рассматривая вышеуказанную дробь, имеем:
(5x2 — 6x — 5)/((x — 1)3(x + 2)) = (A/(x — 1)2) + (C/(x — 1)3)) + (D/(x + 2))
Упрощая выражение путем умножения на (х — 1)3 (х + 2), находим:
5х2 — 6х — 5 = A(х — 1)2(х + 2) + B(x — 1)(x + 2) + C(a + 2) + D(x — 1)3.
Положив здесь х = — 2, находим, что D = — 1.
Положив х = 1, находим, что С = — 2, отсюда
A = 1, В = 2, следовательно
(5х2 — 6x — 5)/((x — 1)3(x + 2)) = 1/(x — 1) + 2/(x — 1)2 — 2/(x — 1)3 — 1/(x + 2)
Правило. Если в знаменателе имеется множитель (х — а)n то данная дробь разлагается на сумму простейших:
A/(x — a) + B/(x — a)2 + C/(x — a)3 + . . . + N/(x — a)n.
Случай № 3
Знаменатель содержит множители второе степени, которые не повторяются и не могут быть разложены на линейные.
Таков, например, знаменатель дроби:
(3x2 — 2)/((x2 + x + 1)(x + 1))
Положим, что
(3x2 — 2)/((x2 + x + 1)(x + 1)) = (Ax + B)/(x2 + x + 1) + C/(x + 1)
Упрощая, имеем:
3x2 — 2 = (Ax + B)(x + 1) + C(x2 + x + 1) = (A + C)x2 + (A + B + C)x + B + C
Применяя способ и сравнивая коэффициенты, находим:
A + C = 3
A + B + C = 0
B + C = -2
отсюда
A = 2, В = -3, С = 1.
Следовательно:
(3x2 — 2)/((x2 + x + 1)(x + 1)) = (2x — 3)/(x2 + x + 1) + (1/x + 1)
Числитель для дроби со знаменателем второй степени берется равным Ax + B, так как знаменатель имеет два корня.
Правило. Если один из множителей знаменателя является многочленом второй степени, то следует предположить, что соответствующая дробь будет иметь вид:
Случай № 4
Знаменатель содержит одинаковые множители второй степени, как например дробь:
Для разложения дроби на простейшие положим, что она равна сумме:
((A/(x — 1)) + ((Bx + C)/(x2 + x + 1)) + ((Dx + E)/(x2 + x + 1)2)
Решение находим точно так же, как к в предыдущем случае.
Правило. Если в знаменателе имеется множитель (ax2 + bx + c)n, то дробь следует представить как сумму простейших:
((Ax + B)/(ax2 + bx + c)) + ((Cx + D)/(ax2 + bx + c)2) + . . . + (Mx + N)/(ax2 + bx + c)n)
Во всех случаях степень числителя каждой простейшей дроби должна быть на единицу меньше, чем степень соответствующего знаменателя.


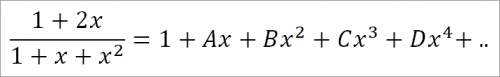
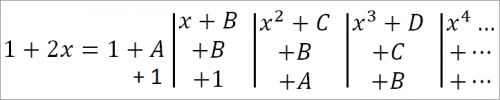
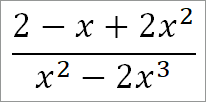
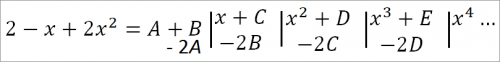
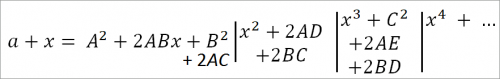
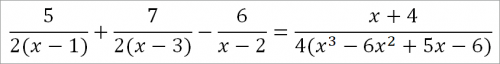
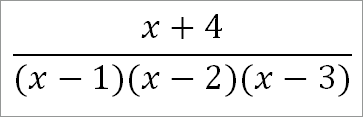
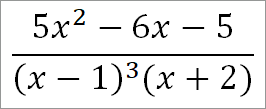
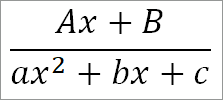
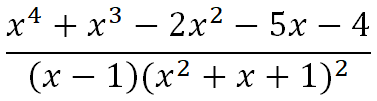
Добавить комментарий
Для отправки комментария вам необходимо авторизоваться.