Теория:
Бумага, на которой нанесена сетка из двух взаимно-перпендикулярных систем линий, расстояние между которыми взято по логарифмической шкале, называется логарифмической бумагой.
Эта бумага весьма удобна для изображения на ней степенных функций.
Чтобы начертить на логарифмической бумаге график функции:
у = ахn, [ур. 1]
возьмем логарифмы обеих частей равенства.
Имеем:
lgy = lga + nlgx.
Положим:
Y = lgy, K =lga, X = lg x.
Тогда вместо ур-ния (1) можно написать:
Y = nХ + К. [ур. 2]
Если принять X и Y за переменные, то ур-нию [2] будет соответствовать прямая линия. Линию того же вида мы получили бы, если бы откладывали значения х и у на логарифмической бумаге.
Действительно, когда мы откладываем какое нибудь значение х, то расстояние от начала координат до точки на оси Х, абсцисса которой равна x, есть нечто иное, как lg х.
Кроме того, наклон прямой, соответствующей ур-нию [2], равен n, т. е. показателю степени при х в ур-нии [1].
Пересечение этой линии с осью Y есть точка с ординатой K, равной lga.
Таким образом, если нанести на логарифмической бумаге значения х и у из [1], то величина n будет характеризоваться наклоном прямой, а значение а можно отсчитать непосредственно на вертикальной шкале.
Логарифмическая шкала
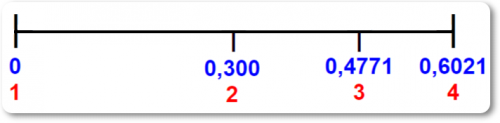
Логарифмическая шкала может быть легко получена, если, вычислив логарифмы чисел от 1 до 10, отложим их в некотором масштабе на прямой (рис. 2).
Вместо значений логарифмов, на полученной шкале следует надписать соответствующие им числа, вследствие чего не будет необходимости разыскивать их в таблицах.
Так например, вместо того, чтобы в начале шкалы писать 0, мы пишем 1, так как 0 есть lg 1; вместо 0,3010 в точке, соответствующей lg 2, мы пишем самое число 2.
Для чего служит логарифмическая бумага
Является удобным средством для выяснения зависимости, связывающей данные, полученные из опыта, если есть основания предполагать, что зависимость между переменными выражается показательной функцией.
Если полученные из опыта данные при нанесении на логарифмическую бумагу, располагаются на прямой линии, то эта линия соответствует степенной функции.
Уравнение, связывающее переменные, можно легко установить, определив место пересечения прямой с осью Y и ее наклон.
Расстояние точки пересечения от начала координат дает коэффициент а, а наклон указывает значение показателя степени в уравнении:
y = axn
Пример решения:
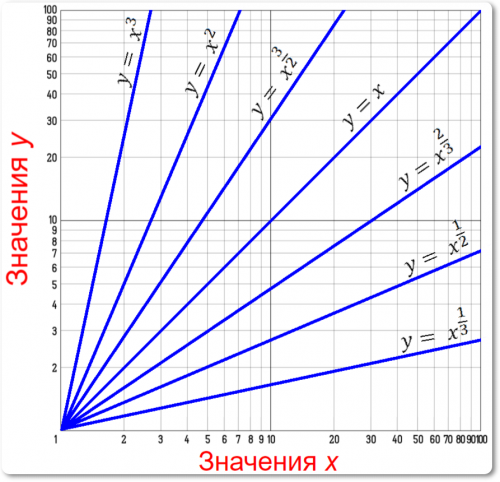
Примеры графиков степенной функции:
Логарифмическая сетка часто наноситься в виде небольших квадратов с делением от 1 до 10 на каждой стороне (рис. 1).
Каждый такой квадрат является повторением такого предыдущего квадрата.
Каждый последующий квадрат соответствует таким образом увеличению логарифма переменной на единицу, что равносильно перенесению запятой один знак вправо.
В случае, если у = х(3/2), то, при перенесении запятой в х на два знака, в у следует перенести ее на три знака, 3 ибо наклон прямой равен 3/2.
С целью экономии места весьма удобно сгруппировать отдельные квадраты в один и таким образом объединить изображение функции на одном квадрате.
Во всех случаях желательно определять положение запятой на-глаз.
После представления функции в логарифмической форме можно продолжать дальнейшие действия как с линейными функциями.
Как было сказано ранее, lg a соответствует точке пересечения с осью Y, n — равен наклону прямой.
Если уравнение функции имеет вид:
y = 3(x + 3)2
то ось Y будет пересекаться прямой в точке 3. Вместо того, чтобы находить lg 3 и откладывать его на оси Y, можно просто отметить эту точку на указанной оси, ибо масштаб подобран таким образом, что точка, отмеченная на оси цифрой 3, соответствует lg 3.
Если вместо х подставить (x + 3), то результат будет отличаться от того, который получился бы в случае прямоугольных координат.
Мы просто вычитаем из чисел, указанных на оси X, три единицы и употребляем для отсчитывания значений х новую шкалу.
Если в уравнении имеется постоянная, изменяющая значение y.
Например:
y = 3(x + 3)2 — 3
или
y + 3 = 3(x + 3)2
то для у — ов следует нанести дополнительную шкалу, так же как это было уже сделано для х — ов.