Вектор (основные понятия физика)

ЧТО ТАКОЕ ВЕКТОРЫ (ОПРЕДЕЛЕНИЕ)

Вектор или векторы — это величины, складываемые геометрическим способом. Они называются «векторами» потому, что их можно охарактеризовать, проведя отрезок прямой, показывающий как величину вектора (в некотором масштабе), так и его направление.

Правило сложения двух векторов

Геометрическое сложение описывается следующим правилом. (Согласно определению векторов, оно автоматически применимо к ним.)

Чтобы сложить два вектора, выбирают подходящий масштаб и вычерчивают их в этом масштабе из одной точки, а затем строят на складываемых векторах параллелограмм. Тогда сумма векторов будет изображаться диагональю параллелограмма, соединяющей исходную точку с противолежащей вершиной.

Рис. Сложение векторов путем построения многоугольника

При таком способе сложения сумма нескольких векторов определяется как единственный вектор, который может заменить первоначальные векторы, или производит такой же физический эффект.

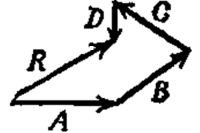
Подобно тому как векторы А и В дают при сложении сумму R₂ (фиг. 45), можно сложить векторы А и В и С, прибавив С к

R₂, в результате чего получим вектор R₃. Прибавляя далее вектор D, получаем R₄ и т. д. Или, проще говоря, любое количество векторов можно складывать, проводя следующий прибавляемый вектор из конца предыдущего, как показано на рис., и их сумма будет изображаться вектором, соединяющим исходную точку с конечной.

Какие величины относятся к векторам? Иначе говоря, какие величины складываются геометрически по правилу параллелограмма? Векторами являются перемещения, или, если называть их более строго, «направленные расстояния» или «смещения». Раз перемещения — векторы, то достаточно разделить их на промежуток времени, за который происходит перемещение, чтобы увидеть, что скорости — тоже векторы. Продолжая этот подход, мы видим, что ускорения — тоже векторы.

Нам встретятся и другие векторы, другие величины, которые нужно измерять с помощью приборов и которые подчиняются правилу геометрического сложения, Здесь возникает важный вопрос: являются ли силы векторами, т.е. подчиняются ли они правилам геометрического сложения? На этот вопрос нельзя ответить, просто подумав. Ответ не очевиден и требует предварительного изучения.

Скаляры

Физические величины, которые имеют только величину и которым нельзя приписать никакого направления, называются скалярами; хорошими примерами скалярных величин служат объем и температура. Существуют и такие вещи, которые не являются ни векторами, ни скалярами, скажем доброта, а также некоторые величины, этакие «сверхвекторы», называемые тензорами. 

Примером тензоров могут служить напряжения в деформированном твердом теле: давление, перпендикулярное к любой площадке образца, и срезающие усилия, действующие вдоль нее. Более сложные примеры встречаются в математической теории относительности.

Например, мы будем рассматривать количество движения т^v как вектор с тремя компонентами: т^v_х, т^v_у, т^v_z, а кинетическую энергию — как скаляр. Эйнштейн, придерживаясь обобщенного представления о пространстве-времени, предпочитал объединять количество движения и кинетическую энергию в «четырехвектор», т. е. с четырьмя компонентами: три для количества движения и одна для кинетической энергии.

Сложение нескольких векторов

Два вектора складываются по правилу параллелограмма. Сложение A + B=R (знаки + и =, напечатанные жирным шрифтом, обозначают геометрическое сложение). Исходя из этого определения, мы можем прийти к более примитивным способам сложения «одного перемещения, а потом другого». Это простейший способ сложения нескольких векторов. Если нам нужно сложить векторы А, В, С, D, то можно было бы складывать их, применяя последовательное построение параллелограмма: получить сумму A+B, прибавить ее к С, а затем прибавить новую сумму к D.

Однако такое построение утомительно, и если выполнить все его этапы на одном чертеже, получится изрядная путаница. Вместо этого сложим А и В по правилам многоугольника, проведя В из конца А, затем прибавим С к их сумме, проведя С из конца этой суммы, затем прибавим D. Можно опустить промежуточные суммы и найти общую сумму R, соединив начало первого вектора с концом последнего.

Проведение параллельных прямых

Чтобы переместить вектор с одного места на листе бумаги в другое, нужно начертить на новом месте отрезок прямой, имеющий ту же длину и то же направление, что и прежний отрезок, т. е. новый отрезок должен быть параллелен первому. Существуют геометрические методы и приспособления, позволяющие провести прямую, параллельную другой прямой. Мы покажем вам

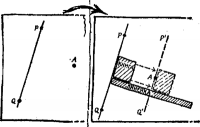
Рис. 2. Простой способ проведения параллельных прямых

хотя бы один способ построения параллельных прямых. Для этого не требуется сложного построения углов.

На рис. 1 показан простой способ проведения параллельных прямых при помощи линейки или обложки книги (или любого прямоугольника или треугольника). Чтобы провести через точку А прямую P’Q’, параллельную прямой Р Q, расположите один край книги вдоль прямой PQ. 

Приложите к другому краю книги линейку. Прижав линейку к бумаге, перемещайте вдоль нее книгу до тех пор, пока та сторона книги, которую вы совместили с прямой PQ, не пройдет через точку А. Теперь проведите по этой стороне требуемую прямую P’Q’ через точку А.