Графики уравнений

  Теория:

Определение функции как некоторой величины у, которая изменяется по мере изменения переменной x, находясь с последней в определенном соотношении.

Величина x есть независимая переменная, а величина у — зависимая переменная.

Точки, находящиеся на прямой линии, служащей основанием, т. е. на оси x-ов, представляют собою значения независимой переменной x.

Переменная же высота кривой линии над осью x-ов выражает значения зависимой переменной у, соответствующие различным значениям независимой переменной х

В большинстве случаев эта высота является переменной величиной, которая показывает как изменяется зависимая переменная по отношению к независимой.

Обычный способ графического изображения функций состоит в том, что на чертеж наносят значения независимой переменной в виде абсцисс, а зависимой — в виде ординат.

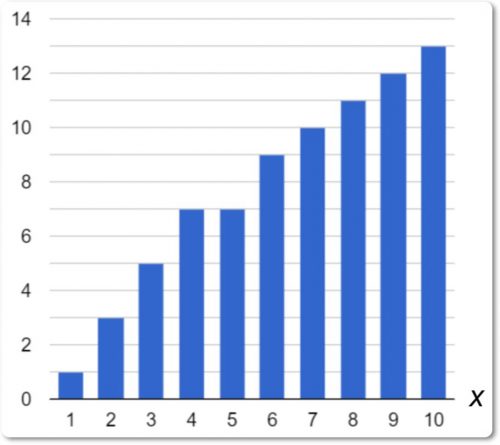
На рис. 1 графически показан характер изменения функции при различных значениях независимой переменной.

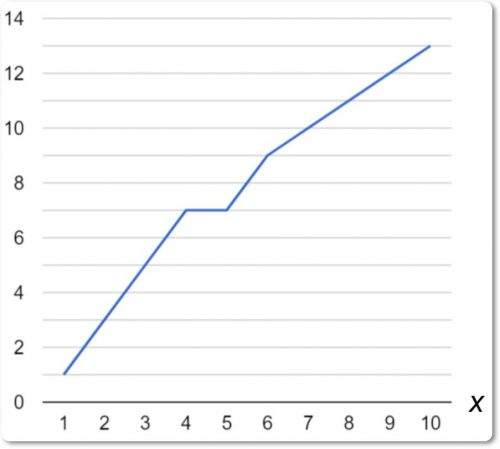
Длина ординаты есть значение величины зависимой переменной, т. е. функции, соответствующей частному значению х (рис. 2).

Чтобы иметь возможность получать величину различных ординат и избежать необходимости вычерчивать их в каждом отдельном случае, проводят кривую, соединяющую их концы, как это показано на рис. 2.

Она представляет собой средство для нахождения величины ординаты для каждого частного значения независимой переменной.

Необходимо помнить, что переменная высота, о которой мы говорим, представляет собой значения функции.

Если имеется выражение:

х² + 3x + 3,

то величина его зависит от значений, которые мы даем независимой переменной х. В таких случаях говорят, что данное выражение есть функция от х.

Построение графика состоит в нанесении на чертеж значений функции, вычисленных для различных х.

  Практика:

Пример решения

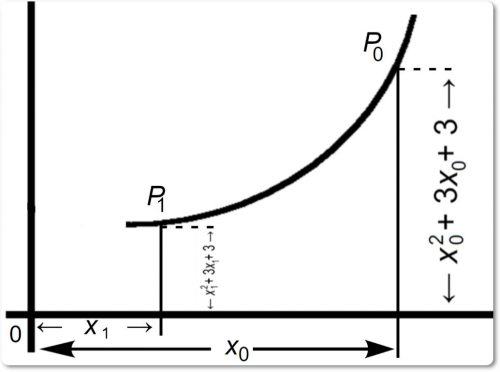
Если читатель усвоит такую точку зрения, то графические соотношения между зависимой и независимой переменными станут для него вполне ясными (рис. 3).

Наше выражение может быть также обозначено через у или другую букву, в таком случае получим равенство:

у = х² + 3х + 3.

Указанное обозначение не изменит первоначального соотношения между абсциссами и ординатами точек кривой, как это видно из рис. 3.