Броуновское движение это случайное движение. Это также может быть отображено более мелкими частицами, которые взвешены в жидкостях.
Броуновское движение возникает в результате столкновений частицы с другими быстро движущимися частицами, присутствующими в жидкости.
Когда две частицы сталкиваются, путь одной частицы будет изменен. Дальнейшее столкновение также заставляет частицу следовать случайному движению, которое называется зигзагообразным.
В ходе этого процесса между частицами происходит обмен импульсом и энергией.
Что такое броуновское движение
Броуновское движение было названо в честь шотландского ботаника Роберта Брауна, который первым заметил, что при помещении в воду-пыльцевые зерна движутся в случайных направлениях.
Биологически броуновское движение происходит, когда частица движется случайным образом зигзагообразно, что можно наблюдать под мощным микроскопом.
Подобное движение описано Робертом Брауном как броуновское движение и напоминает движение пыльцевых зерен в воде.
Броуновское движение пыльцы позже было разъяснено Альбертом Эйнштейном в его работе, объяснив, что пыльца перемещалась молекулами воды. Это открытие укрепило молекулярное и атомное существование.
Современная атомная теория основана на броуновском движении, которое необходимо понять. Кроме того, кинетическая теория газов основана на модели броуновского движения частиц.
Математические модели, описывающие броуновское движение, используются в различных дисциплинах, таких как физика, математика, экономика, химия и многое другое.
Что такое броуновское движение в химии
Броуновское движение в химии, которое также называют броуновским движением, можно определить как беспорядочное или неконтролируемое движение частиц в жидкости из-за их постоянного столкновения с другими быстро движущимися молекулами.
В общем случае можно наблюдать, что это случайное движение частицы сильнее в менее вязкой жидкости, частицах меньшего размера и при более высокой температуре.
Существуют также другие факторы, влияющие на движение частиц в жидкости.
Одним из таких наиболее распространенных примеров броуновского движения можно привести диффузию.
Примерами такого эффекта можно считать случаи, когда кальций рассеивается в костях или загрязняющие вещества рассеиваются в воздухе.
Броуновское движение в коллоидах
Мы можем видеть эффект броуновского движения во всех типах коллоидного золя. С другой стороны, это явление ясно объясняет случайное движение частиц золя и указывает на то, что эти частицы не статичны.
Тем не менее, основной причиной такого типа движения частиц золя является неравномерная бомбардировка частицы подавленной фазы, приводящая к неравномерному движению в среде из-за разницы в размерах частиц.
Между тем броуновское движение нельзя увидеть в истинном решении, потому что оно однородно, и в этом заключается равномерная бомбардировка.
Однако, учитывая коллоиды, система неоднородна, а бомбардировки неоднородны, что приводит к случайному измерению.
Одним из основных преимуществ этого эффекта является то, что он удерживает частицы золя в непрерывном движении, поэтому частицы не оседают на дне, дополнительно предотвращая коагуляцию лиофобных золей.
Таким образом, этот тип движения повышает стабильность золя. Броуновское движение также можно наблюдать в плазме клетки, где частицы в клетке также существуют в случайном движении, не делая плазму в клетке сухой.
Причина Броуновского движения
Основные причины броуновского движения можно перечислить следующим образом:
-
Размер частицы обратно пропорционален скорости движения, что означает, что мелкие частицы демонстрируют более быстрые движения.
-
Это связано с тем, что передача импульса обратно пропорциональна массе частиц. В то же время более легкие частицы получают большие скорости от столкновений.
-
Скорость броуновского движения обратно пропорциональна вязкости жидкости: чем ниже вязкость жидкости, тем быстрее происходит броуновское движение.
-
Вязкость может быть задана как величина, выражающая величину внутреннего трения в жидкости. Это мера сопротивления для потока жидкости.
Эффекты броуновского движения:
-
Броуновское движение приводит к тому, что частицы жидкости находятся в постоянном движении.
-
Это предотвращает оседание частиц, что приводит к стабильности коллоидного золя.
-
С помощью этого движения мы можем отличить настоящий золь от коллоида.
Статья Альберта Эйнштейна о броуновском движении дает существенные доказательства существования молекул и атомов.
В кинетической теории газов частицы модели броуновского движения отвечают за описание температуры, объема и давления.
Кто открыл Броуновское движение
В дальнейшем оказалось, что это движение свойственно любым мельчайшим частицам как органического, так и неорганического происхождения и проявляется тем интенсивнее, чем меньше масса частиц, выше температура и ниже вязкость среды.
Открытию Броуна долгое время не придавали особого значения. Большинство ученых считали причиной беспорядочного движения частиц дрожание аппаратуры и наличие конвективных потоков в жидкости.
Однако тщательные опыты, проведенные во второй половине прошлого века, показали, что, какие бы меры ни принимали для соблюдения механического и теплового равновесия в системе.
Броуновское движение проявляется при данной температуре всегда с одинаковой интенсивностью и неизменно во времени.
Крупные частицы смещаются незначительно; для более мелких характерно беспорядочное по своему направлению движение по сложным траекториям.
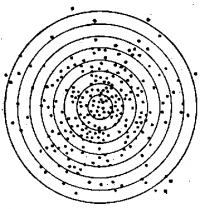
Рис. Распределение конечных точек горизонтальных смещений частицы, находящейся в броуновском движении (начальные точки смещены в центр).
Почему образуется Броуновское движение
Напрашивался следующий вывод:
Броуновское движение обусловлено не внешними, а внутренними причинами, а именно — столкновением молекул жидкости со взвешенными частицами.
Ударяясь о твердую частицу, каждая молекула передает ей часть своего количества движения (mυ).
Вследствие полной хаотичности теплового движения суммарный импульс, полученный частицей за большой промежуток времени, равен нулю.
Однако в любой достаточно малый отрезок времени ∆t импульс, полученный частицей с какой-либо одной стороны, всегда будет больше, чем с другой. В результате происходит ее смещение.
Доказательство этой гипотезы имело в то время (конец XIX — начало XX в.) особенно большое значение, поскольку некоторые естествоиспытатели и философы, например Оствальд, Мах, Авенариус, сомневались в реальности существования атомов и молекул.
Вывод уравнения движения
В 1905—1906 гг. А. Эйнштейн и польский физик Мариан Смолуховский независимо друг от друга создали статистическую теорию броуновского движения, приняв в качестве основного постулата предположение о его полной хаотичности.
Для сферических частиц ими было выведено уравнение:
где ∆x — средний сдвиг частицы за время t (т. е. величина отрезка, соединяющего начальное положение частицы с ее положением в момент t); η — коэффициент вязкости среды; r — радиус частицы; Т — температура в К; N0 — число Авогадро; R — универсальная газовая постоянная.
Полученное соотношение было проверено экспериментально Ж. Перреном, которому для этого пришлось изучить броуновское движение сферических частиц гуммигута, камеди и мастики с точно известным радиусом.
Фотографируя последовательно одну и ту же частицу через равные промежутки времени, Ж. Перрен находил значения ∆x для каждого ∆t.
Результаты, полученные им для частиц разных размеров и различной природы, очень хорошо совпали с теоретическими, что явилось прекрасным доказательством реальности атомов и молекул и еще одним подтверждением молекулярной-кинетической теории.
Отмечая последовательно положение движущейся частицы через равные промежутки времени, можно построить траекторию броуновского движения.
Если провести параллельный перенос всех отрезков так, чтобы их начальные точки совпадали, то для конечных точек получается распределение, аналогичное разбросу пуль при стрельбе в мишень (рис.).
Это подтверждает основной постулат теории Эйнштейна — Смолуховского — полную хаотичность броуновского движения.
Кинетическая устойчивость дисперсных систем
Обладая определенной массой, взвешенные в жидкости частицы должны в гравитационном поле Земли постепенно оседать (если их плотность d больше плотности окружающей среды d0) или всплывать (если d<d0). Однако этот процесс полностью никогда не происходит.
Оседанию (или всплыванию) препятствует броуновское движение, стремящееся распределить частицы равномерно по всему объему. Скорость оседания частиц зависит поэтому от их массы и от вязкости жидкости.
Например, шарики серебра диаметром 2 мм проходят в воде 1 см за 0,05 сек, а диаметром 20 мкм — за 500 сек. Как видно из таблицы, частицы серебра диаметром менее 1 мкм вообще не способны осесть на дно сосуда.
Сравнение интенсивности броуновского движения и скорости оседания частиц серебра (расчет Бертона)
| Расстояние, проходимое частицей за 1 сек. мк | ||
| Диаметр частиц, мкм | Броуновское движение | Оседание |
| 100 | 10 | 6760 |
| 10 | 31,6 | 67,6 |
| 1 | 100 | 0,676 |
Если дисперсная фаза за сравнительно короткое время оседает на дно сосуда или всплывает на поверхность, то систему называют кинетически неустойчивой.
Примером может служить суспензия песка в воде.
Если частицы достаточно малы и броуновское движение препятствует их полному осаждению, систему называют кинетически устойчивой.
Вследствие беспорядочного броуновского движения в кинетически устойчивой дисперсной системе устанавливается неодинаковое распределение частиц по высоте вдоль действия силы тяжести.
Характер распределения описывается уравнением:
где с1 — концентрация частиц на высоте h1; с2— концентрация частиц на высоте h2; т — масса частиц; d — их плотность; D0— плотность дисперсионной среды.
С помощью этого уравнения впервые была определена важнейшая константа молекулярно-кинетической теории — число Авогадро N0.
Подсчитав под микроскопом количество взвешенных в воде частиц гуммигута на различных уровнях, Ж. Перрен получил численное значение константы N0, которое изменялось в различных опытах от 6,5 • 1023 до 7,2 • 1023.
По современным данным число Авогадро равно 6.02 • 1023.
В настоящее время, когда константа N0 известна е очень большой точностью, подсчет частиц на различных уровнях используют для нахождения их размера и массы.
Часто задаваемые вопросы ответы о броуновском движении?
Пример броуновского движения?
Примеры броуновского движения: Броуновское движение в основном наблюдается в транспортных системах, которые подвержены воздействию больших токов и в то же время проявляют педезис.
Например, движение пыльцевых зерен по неподвижному водоему. Диффузия загрязняющих веществ в воздухе вызвана частицами пыли, движущимися в помещении, обычно вызванными воздушными потоками.
Как возникает броуновское движение?
Броуновское движение возникает, когда частицы сталкиваются с окружающими молекулами, заставляя их двигаться случайным образом.
Индуцированная диффузия частиц происходит, когда градиент концентрации вызывает движение частиц. Это движение происходит, когда частицы смещаются от высоких концентраций к низким.
Как работает броуновское движение в газе?
Независимо от того, является ли вещество жидким или газообразным (в совокупности называемым жидкостью), частицы движутся случайным образом. За это отвечает броуновское движение.
В жидкостях движущиеся частицы бомбардируют эти частицы, заставляя их вести себя подобным образом. Более крупные частицы могут перемещаться молекулами, которые движутся быстро.
Почему реальное решение не следует за броуновским движением?
Истинные растворы содержат более мелкие, однородные частицы растворенного вещества. Эти частицы движутся равномерно и не проявляют броуновского движения.
Что вызывает броуновское движение в коллоидном растворе?
Коллоидные “растворы” состоят из мельчайших частиц (твердых или жидких), которые нельзя увидеть невооруженным глазом, но можно увидеть через микроскоп, взвешенных в жидкой среде (растворителе). Они не являются истинными решениями.
Например, молоко. Молоко состоит из мельчайших частиц жира, взвешенных в воде. Частицы жира рассеивают свет и их можно увидеть. Теперь вопрос в том, почему молоко кажется “молочным”? (непрозрачный и белый) и не похож на воду?
Таким образом, вы можете наблюдать броуновское движение, когда частицы жира то тут, то там ударяются молекулами воды.
В чем разница между броуновским движением и подвижностью?
Может быть довольно сложно отличить движение, вызванное броуновским движением, от движения, вызванного другими эффектами.
В биологии, например, наблюдатель должен быть в состоянии определить, движется ли образец, потому что он подвижен (способен двигаться самостоятельно, возможно, из-за ресничек или жгутиков) или потому, что он подвержен броуновскому движению.
Как правило, можно представить себе разделение процессов, потому что броуновское движение кажется скачкообразным, случайным или похожим на вибрацию.
Истинная подвижность часто проявляется как путь, или же движение извивается или поворачивается в определенном направлении. В микробиологии подвижность может быть установлена, если культура, привитая в полутвердой среде, отклоняется от линии укола.


