Движение тела

Движение тела брошенного горизонтально и под углом к горизонту

Тело, брошенное горизонтально, совершает сложное движение, состоящее из двух простых: равномерного движения в горизонтальном направлении со скоростью υ и свободного падения с высоты H, на которой находилось тело в момент бросания (рис. 1). Эти два движения не зависят друг от друга. Полное время движения определяется временем падения тела с высоты Н

t = √(2H/g)

Путь, пройденный в горизонтальном направлении, можно определить по уравнению равномерного движения:

s = υt = υ√(2H/g)

Траекторией движения будет часть параболы.

Движение тела брошенного под углом к горизонту

Движение тела, брошенного под углом к горизонту, также сложное, состоящее из двух независимых простых движений: равномерного движения в горизонтальном направлении и движения в вертикальном направлении.

Это движение до точки наивысшего подъема над Землей будет равно-замедленным и после прохождения точки наивысшего подъема равноускоренным (если не учитывать сопротивления воздуха, то свободным падением).

Траекторией этого сложного движения будет парабола.

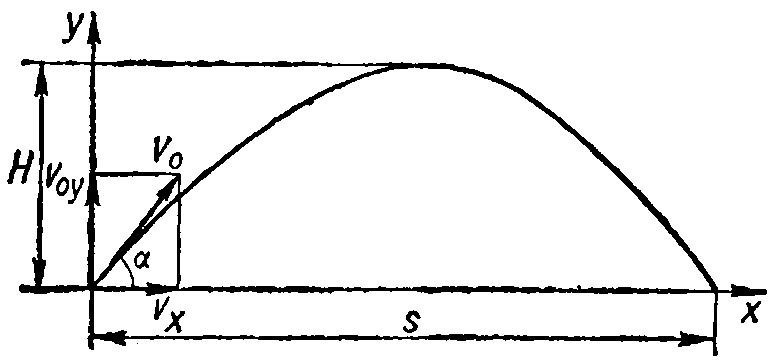
Разложим начальную скорость υ₀, с которой бросают тело, на горизонтальную и вертикальную составляющие.

В этом случае движение рассматривается относительно Земли, поэтому за систему отсчета принимается Земля и прямоугольная система координат связывается с Землей.

Согласно обозначениям, принятым на рис. 2,

υ_х = υ₀ cosα,

υ_0y = υ₀ sin α

Движение тела в вертикальном направлении

Движение тела в вертикальном направлении до точки наивысшего подъема подчиняется уравнению равно-замедленного движения:

Н = υ_0yt₁ — ((gt²₁)/2)

В верхней точке вертикальная скорость равна нулю, поэтому:

υ_y = υ_0y — gt₁ = 0,

где t₁— время подъема, g—ускорение силы тяжести (знак «минус» показывает, что ускорение g направлено в противоположную скорости υ_y сторону).

Подставляя (2) в (3) и (4), получим:

Н = υ₀ sin α • t₁ — ((gt²₁)/2)

υ₀ sin α — gt₁ = 0.

Отсюда определим время подъема:

t₁ = (υ₀ sin α)/g

и наибольшую высоту подъема тела над Землей:

Н_макс = ((υ₀ sin² α)/g) — ((gυ²₀ sin² α)/2g²)

Так как время подъема t₁ равно времени падения t₂, то полное время движения тела:

t = t₁ + t₂ = (2υ₀ sin α)/g

В горизонтальном направлении

Движение тела в горизонтальном направлении равномерное, и за время t тело в этом направлении проходит путь:

s = υ_xt = υ₀ cos α ((2υ₀ sin α)/g), или s = (υ²₀ sin 2α)/g)

Как видно, дальность полета зависит от угла, под которым бросают тело. Очевидно, наибольшая дальность полета будет при sin 2α = 1, отсюда α = 45°, тогда:

s_макс = υ²₀/g

Чтобы определить вид траектории, рассмотрим уравнения:

s = υ₀cos αt и H = υ₀cos αt1 — (gt²₁/2)

Решаем совместно эти уравнения, учитывая, что t₁ = t/2 предварительно заменив s на х, а Н на y.

Получим уравнение траектории:

y = (1/2)tgαx — (g/8υ²₀ cos²α) • x²

коэффициенты при х и х² обозначим через а и b:

1/2tg,α = a, g/8υ²₀ cos²α = b

тогда уравнение примет вид:

— bx² + ах = у.

Таким образом, траектория движения тела, брошенного под углом к горизонту, представляет собой параболу.

Однако сопротивление воздуха уменьшает как дальность полета, так и наибольшую высоту полета, и траектория становится несимметричной.

Такая кривая называется баллистической.

Сопротивление воздуха уменьшает дальность полета примерно в 10 раз.