Рене Декарт
Следует, однако, подчеркнуть, что было бы грубым упрощением считать Декарта основателем дедуктивного метода, а Бэкона — основателем индуктивного. Оба метода зародились еще в древней Греции, и Бэкон и Декарт лишь развили их применительно к естествознанию. При этом ни Бэкон не отрицал значения дедукции, ни Декарт не отрицал значения опыта и индукции. Научный метод основан на диалектическом сочетании индукции и дедукции, и это понимали оба великих философа. Но Бэкон подчеркивал ведущую роль опыта и индукции, Декарт же — логического анализа и правильных умозаключений. Он полагал, что в основу этих умозаключений должны быть положены ясные и простые принципы и строгая логическая последовательность выводов. Математика в методе Декарта играет первостепенную роль. Он писал: «Те длинные цепи выводов, сплошь легких, простых, которыми пользуются геометры, чтобы дойти до своих наиболее трудных доказательств, дали мне повод представить себе, что и все вещи, которые могут стать предметом знания людей, находятся между собой в такой же последовательности. Таким образом, если остерегаться принимать за истинное что-либо, что таковым не является, и всегда наблюдать порядок, в каком следует выводить одно из другого, то не может существовать истин ни столь отдаленных, чтобы они не были недостижимы, ни столь сокровенных, чтобы нельзя было их раскрыть».
Таким образом, Декарт, применяя метод геометров, т. е. математиков, можно добиться в изучении природы огромных успехов. Для этого метода нет недостижимых истин, «столь сокровенных, чтобы нельзя было их раскрыть». Эта вера в мощь математического метода весьма характерна для Декарта, и он особенно ценил Галилея за то, что тот «старается изучать вопросы с помощью математического рассуждения».
Но основной проблемой физики XVII в. были законы движения. Как применить математику к движению? И здесь Декарту принадлежит решающее открытие: он ввел в математику переменные величины, установил соответствие между геометрическими образами и алгебраическими уравнениями; Декарт положил начало аналитической геометрии. Здесь он впервые применил свой метод: «Приняв во внимание, что среди всех искавших истину в науках только математикам удалось найти некоторые доказательства, т. е. некоторые точные и очевидные соображения, я не сомневался, что и мне следовало начать с того, что было ими обследовано». Результатом такого начала явилась «геометрия», приложенная к «Рассуждению о методе». Другими приложениями являются «Диоптрика» и «Метеоры».
Когда идея или открытие назревает, она возникает почти одновременно в нескольких головах. Так было и с идеей переменной величины. Галилей в своих механических исследованиях хорошо понимал необходимость оперирования переменными величинами. Идея мгновенной скорости, меняющейся от момента к моменту, была им освоена во всей полноте. В «Диалоге» Он описывает, как свободно падающее тело проходит через все ступени скорости, начиная с нулевой. Собеседники не сразу могут принять эту идею, им трудно понять, что падающее ядро обладает вначале такой скоростью, что, сохранись она неизменной, ядро не достигло бы Земли и за день. Сальвиати подхватывает эту мысль, усиливает ее:(Можете сказать в год, в десять, а тысячу лет)
В «Беседах» обсуждение переменной скорости падающего тела занимает видное место. Сагредо вновь возвращается к своей мысли: «Надлежит признать, что дли промежутков времени, все более и более близких К моменту выхода тела из состояния покоя, мы придем к столь медленному движению, что при сохранений постоянства скорости тело не пройдет мили ни в час, ни в день, ни в год, ни даже в тысячу лет; даже в большее время оно не продвинется и на толщину пальца — явление, которое весьма трудно себе представить, особенно, когда наши чувства показывают, что тяжелое падающее тело сразу же приобретает большую скорость». Сальвиати подробно разъясняет это обстоятельство и, в частности, указывает, что при бросании тела вверх оно постоянно уменьшает свою скорость до полной остановки. Симлличио возражает в духе апорий Зенона, что невозможно исчерпать бесконечное количество степеней медленности и, таким образом, брошенное вверх тело никогда не останавливается. Возражение Симпличио Сальвиати парирует чрезвычайно сильно: «Это случилось бы, синьор Симпличио, если бы тело двигалось с каждой степенью скорости некоторое определенное время, но оно только проходит через эти степени, не задерживаясь более чем на мгновение, а так как в каждом, даже самоммалом, промежутке времени содержится множество мгновений, то их число является достаточным для соответствия бесконечному множеству степеней скорости».
Как видно из этого опыта, Галилей отчетливо представляет текучесть переменной величины, которая проходит последовательно все значения и не задерживается «более чем на мгновение». Мгновение — бесконечно малая величина, число мгновений даже в небольшом промежутке времени бесконечно велико и взаимно однозначно соответствует числу значений переменной величины. Галилей владеет идеей взаимно однозначного соответствия бесконечных множеств. Это видно, например, из его утверждении, что всех членов натурального ряда чисел«столько же», сколько полных квадратов этих чисел.
Галилей независимо от Декарта пришел к идее представления переменной величины линией. Этой идеей он пользовался для вывода закона пути равноускоренного движения. Он разработал остроумный метод измерения конечной скорости падающего тела по глубине ямки, оставленной в мягкой пластине упавшим телом. Установив, что эта глубина Пропорциональна высоте падения, Галилей пришел сначала к ошибочному выводу, что скорость падающего тела пропорциональна пройденному пути. Но он скоро понял свою ошибку и установил, что в равноускоренном движении скорость пропорциональна времени. Изображая время отрезками вертикальной прямой, он изображал скорость, полученную телом в конце данного промежутка времени, отрезком перпендикуляра к оси времен, восстановленного в конце соответствующего отрезка времени.
Таким образом, Галилей впервые изобразил зависимость скорости от времени графически, и его график отличается от принятого ныне только тем, что время мы откладываем теперь по горизонтальной оси, а скорость— по вертикальной, что, конечно, совершенно несущественно. Путь, пройденный телом за данный промежуток времени, Галилей определяет по графику, суммируя все отрезки скорости, т. е. величину площади фигуры (в случае равномерного движения — прямоугольника, в случае равноускоренного движения — прямоугольного треугольника), образованной графиком скорости, осью времен и начальным и конечным отрезками скорости, т. е. по существу выполняет операцию интегрирования.
Ученики Галилея Кавальери и Торричелли также внесли свой вклад в основание теории бесконечно малых. Дело создания основ математики переменных величин было завершено Ньютоном и Лейбницем.
Вернемся, однако, к Декарту. В 1644 г. Декарт издал обширное сочинение под названием «Начала философии». В него вошли части сочинения Декарта о мире (космосе), которое он намеревался издать еще в 1633 г. Услышав об осуждении Галилея, он отложил издание своего сочинения и только спустя одиннадцать лет обнародовал его в расширенном и переработанном виде. В этом сочинении он изложил грандиозную программу создания теории природы, руководствуясь своим методологически» правилом брать за основу наиболее простые и ясные положения, Еще в «Рассуждении о методе» Декарт подверг анализу всевозможные исходные положения, сомневаясь в справедливости любого из них, в том числе и в положении «Я существую». Однако в акте мышления сомнение невозможно, ибо наше сомнение уже есть мысль. Отсюда знаменитое положение Декарта: «Я мыслю — следовательно существую». Чтобы обезопасить свое учение от нападок церковников, Декарт говорит о существовании бога и внешнего мира, созданного богом. Но обмануть церковников не удается, они распознали материалистическую сущность системы Декарта, и ученому под конец жизни пришлось искать убежища в Швеции, где он и умер. Верный своему методу, Декарт ищет в материальном субстрате самое основное и простое и находит его в протяженности.
Материя Декарта — это чистая протяженность, материальное пространство, заполняющее всю безмерную длину, ширину и глубину Вселенной. Части материи находятся в непрерывном движении, взаимодействуя друг с другом при контакте. Взаимодействие материальных частиц подчиняется основным законам или правилам.
«Первое правило состоит в том, что каждая часть материи по отдельности всегда продолжает оставаться в одном и том же состоянии до тех пор, пока встреча с другими частицами не вызовет изменения этого состояния».
«Второе правило, предполагаемое мною, заключается в следующем: когда одно тело сталкивается с другим, оно может сообщить ему лишь столько движения, сколько само одновременно потеряет, и отнять у него лишь столько, насколько оно увеличит свое собственное движение».
«В виде третьего правила я прибавлю, что хотя при движении тела его путь чаще всего представляется в виде кривой линии и что невозможно произвести… ни одного движения, которое не было в каком-либо виде круговым, тем не менее каждая из частиц тела по отдельности стремится продолжать тело по прямой линии».
В этих «правилах» обычно усматривают формулировку закона инерции и закона сохранения количества движения. В отличие от Галилея Декарт отвлекается от действия тяготения, которое он, между прочим, также сводит к движению и взаимодействию частиц, и упоминает о направлении инерционного движения по прямой. Однако его формулировка еще отличается от ньютоновской, он говорит не о состоянии равномерного и прямолинейного движения, а вообще о состоянии, не разъясняя подробно содержания этого термина.
Из всего содержания «Начал» видно, что состояние частей материи характеризуется их величиной («количество материи»), формой, скоростью движения и способностью изменять эту скорость под воздействием внешних частиц. Можно отождествить эту способность с инерцией, и тогда в одном из писем Декарта мы встречаем очень интересное утверждение. «Можно утверждать с достоверностью, что камень неодинаково расположен к принятию нового движения или к увеличению скорости, когда он движется очень скоро и когда он движется очень медленно».
Другими словами, Декарт утверждает, что инерция тела зависит от его скорости. Известный русский физик Н. А. Умов, приводя в 1896 г. эту выдержку, подчеркнул важность утверждения Декарта и высказал мысль, что при скоростях, близких к скорости света, масса тела должна возрастать. Как известно, закон возрастания массы со скоростью был установлен в теории относительности Эйнштейном, а для электромагнитной инерции — Д. Д. Томсоном.
В письмах Декарта встречается формулировка закона инерции, уже почти текстуально совпадающая с ньютоновской: «Полагаю, что природа движения такова, что, если тело пришло в движение, уже этого достаточно, чтобы оно его продолжало с той же скоростью и в направлении той же прямой линии, пока оно не будет остановлено или отклонено какой-либо другой причиной».
Этот принцип сохранения скорости по величине и направлению тем более интересен у Декарта, что, по его представлению, в мире пустоты нет и всякое движение является циклическим: одна часть материи занимает место другой, эта — предыдущей и т. д. В результате вся Вселенная пронизана вихревыми движениями материи. Движение во Вселенной вечно, так же как и сама материя (хотя Декарт и пишет о сотворении материи и движения богом, но в дальнейшем бог устраняется и природа действует по собственным законам), и все явления в мире сводятся к движениям частиц материи. Вначале эти движения были хаотическими и беспорядочными, в результате этих движений частицы дробились и сортировались.
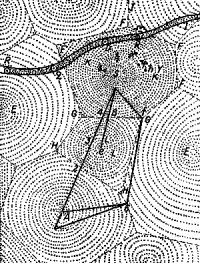
По Декарту, существуют три сорта частиц (три элемента): частицы земли, воздуха (неба), огня. Наиболее крупные частицы — это частицы земли. Они погружены в среду из частиц неба, в которые вкраплены также частицы огня, образующие Солнце. Вихревые движения круглых подвижных частиц «неба» увлекают в своем движении планеты, состоящие из элементов земли. Вся Вселенная разбита на такие вихревые области, которые можно рассматривать как предшественники современных галактик. Такова космогоническая гипотеза Декарта.
В физике Декарта нет места силам, тем более силам, действующим на расстоянии через пустоту. Все явления мира сводятся к движениям и взаимодействию соприкасающихся частиц. Такое физическое воззрение получило в истории науки название картезианского, от латинского произношения имени Декарта — Картезий. Картезианское воззрение сыграло огромную роль в эволюции физики и, хотя и в сильно измененной форме, сохранилось до нашего времени. Все попытки построить единую теорию поля и вещества по существу повторяют на новой основе попытку Декарта построить физическую картину мира с непрерывной материей и сохраняющимся механическим движением.
Статья на тему Рене Декарт


Добавить комментарий
Для отправки комментария вам необходимо авторизоваться.