Равномерное движение по окружности

Что такое равномерное движение по окружности

При равномерном движении точки по окружности линейная скорость, с которой эта точка движется по окружности, постоянна по своей величине, но направление скорости меняется: линейные скорости различных точек всегда направлены по касательной к траектории движения.

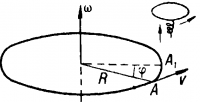
Для характеристики вращательного движения, кроме линейной скорости, характеризующей линейное перемещение точки, вводится понятие угловой скорости. Пусть точка А равномерно вращается по окружности радиуса R. В какой-то момент времени точка находилась в положений A, а через промежуток времени t оказалась в положении A₁, то есть за время t точка повернулась на угол φ (рис.).

Угловая скорость

Это — физическая величина, равная отношению угла поворота радиуса к промежутку времени, за который произошел поворот, называется угловой скоростью. Она обозначается буквой ω.

ω = φ/t

В единицах СИ угловая скорость измеряется в рад/с. Угловая скорость — векторная величина, ее направление определяется по правилу буравчика: если вращение головки буравчика совпадает с направлением вращения точки по окружности, то поступательное движение буравчика покажет направление вектора угловой скорости. Вектор со направлен вдоль оси вращения и приложен в центре вращения (рис.).

Период вращения

Время, в течение которого точка, двигаясь по окружности, совершает один оборот, называется периодом и обозначается Т,

Т = 1/n

где n — число оборотов в 1с. Выразим угловую скорость через число оборотов в 1с и период.

Если тело за время t = 1с делает один оборот, то φ = 2π. Подставив в формулу ω = φ/t получим ω = 2n; если тело за 1с делает n оборотов, то ω = 2πn. Учитывая, что n = 1/Т можно получить

ω = 2π/Т.

Установим связь между линейной и угловой Скоростями при равномерном вращении точки по окружности. Линейная скорость υ = s/t. Точка, двигаясь по окружности и делая один оборот за 1с, пройдет путь s = 2πR. Если тело совершит за 1с n оборотов, то

υ = 2πRn, или υ = (2πR)/Т

Сравнивая выражения линейной и угловой скорости, получим

υ = ωR.

Из формул ω = 2πn и υ = 2πRn видно, что для всех точек вращающегося тела угловая скорость — величина постоянная; а линейная скорость зависит от радиуса вращения: чем дальше точка расположена от оси вращения, тем больше ее линейная скорость.

Выше было сказано, что при равномерном вращении точки по окружности величина линейной скорости остается постоянной, а направление изменяется. Но изменение скорости в единицу времени и есть ускорение. Следовательно, при равномерном вращении по окружности точка движется с ускорением, которое обусловливает изменение скорости по направлению.

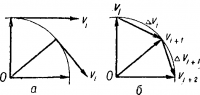
Такое ускорение называется центростремительным. Вектор центростремительного ускорения направлен к центру вращения. Для определения этого ускорения разобьем период движения Т на n малых, равных между собой, промежутков ∆t_i (i = 1, 2,n).

В начале каждого из этих промежутков времени, точка имела какую-то скорость υ_i. Скорости υ_i направлены по касательной к данной точке траектории и по абсолютной величине равны между собой, так как рассматриваемое движение равномерное (рис. 2, а).

Векторы ∆υ_i. равные разности векторов υ_{i + 1} и υ_i образуют многоугольник, число углов которого n (рис. 2, б). Опишем многоугольник окружностью, радиус которой численно равен линейной скорости (R = υ). Вычислим модуль приращения скорости за период Т

так как R = υ. Следовательно

a = ∆υ/T = (2πυ)/(2πR/υ) = υ2/R

Выражая линейную скорость через угловую (υ = ωR), получим

а = υ²/R = ω²R²/R = ω²R

Если тело движется с ускорением, то на него (по второму закону Ньютона) действует сила, в данном случае эту силу будем называть центростремительной.

Статья на тему Равномерное движение по окружности