ЧТО ТАКОЕ ЗАКОН СОХРАНЕНИЯ ИМПУЛЬСА ДЛЯ ЗАМКНУТОЙ СИСТЕМЫ
Рассмотрим замкнутую систему, состоящую из n тел. По второму закону Ньютона каждое тело, входящее в систему, взаимодействует со всеми телами, кроме самого себя. Так, первое тело взаимодействует со вторым, третьим и т. д. Для этого взаимодействия второй закон можно записать так:
∆(m1υ1)/∆t = F12 + F13 + … + F1n
где F12 —сила взаимодействия первого тела со вторым, F13 —сила взаимодействия первого тела с третьим и т. д.
Закон сохранения импульса примеры
Аналогично запишем второй закон Ньютона для взаимодействия второго тела со всеми другими телами, входящими в систему, затем третьего тела со всеми другими и т. д.
Тогда получим:
∆(m2υ2)/∆t = F21 + F23 + … + F2n
∆(m3υ3)/∆t = F31 + F32 + … + F3n
∆(mnυn)/∆t = Fn1 + Fn2 + … + Fn(n — 1)
где F21, F23, …, F2n и т.. д. — силы взаимодействия второго тела с первым, второго тела с третьим и т. д.
Полученные равенства сложим почленно, предварительно сгруппировав силы с противоположными индексами
(∆(m1υ1)/∆t) + (∆(m2υ2)/∆t) + … + (∆(mnυn)/∆t) = (F12 + F21) + (F13 + F31) + … + (F1n + Fn1)
где индекс i показывает номер слагаемого, an — число слагаемых, Но по третьему закону Ньютона:
F12= — F21; F13 = F31 и т. д.
Тогда
∆t ≠ 0, следовательно, можно записать, что
Не трудно видеть, что
Пусть скорости частиц υ1, υ2, υ3, …,υn изменились и стали υ1‘, υ2‘, υ3‘, …, υn тогда, с одной стороны,
с другой стороны,
Равенство (выше) получим, раскрыв скобки в выражении (перед ним) и сгруппировав скорости после действия силы (со штрихом) и скорости до действия силы (без штриха).
Известно, что если изменение какой-либо величины равно нулю, то эта величина есть постоянная, поэтому
Вывод чему равна сумма импульсов : сумма импульсов тел изолированной системы есть величина постоянная.
В результате взаимодействия импульс замкнутой системы тел не изменяется. Из (1), (2), (3) следует, что равнодействующая всех сил, действующих внутри замкнутой системы, равна нулю и осуществить движение системы в целом эти силы не могут.
Этот закон более элементарно можно вывести так. Имеем взаимодействие двух тел массами m1 и m2, движущихся до взаимодействия со скоростями υ1 и υ2. Пусть после взаимодействия их скорости станут u1 и u2. Время взаимодействия t. Во время взаимодействия тел возникают силы, равные по величине и противоположные по направлению (по третьему закону):
F1 = — F2
Согласно второму закону,
F1 = m1а1 но а1 = (u1 — υ1)/ t.
F2 = m2a2, но а2 = (u2 — υ2)/ t.
Исходя из этого, можно записать
m1((u1 — υ1)/ t) = m2((u2 — υ2)/ t).
Закон сохранения импульса формула
После преобразования получим
m1υ1 + m2υ2 = m1u1 + m2u2
Чему равна она равна : сумма импульсов тел до взаимодействия равна сумме импульсов тел после взаимодействия.
Примером применения закона импульса в технике является работа реактивных двигателей. Если внутри ракеты происходит сгорание горючего вещества, то образовавшиеся газы с большой скоростью устремляются наружу, унося с собой какой-то импульс силы.
В то же время сама ракета движется в противоположную сторону с такой скоростью, которая соответствует сумме импульсов ракеты и газа после начала движения ракеты, равной сумме импульсов тел этой же системы до начала движения ракеты.


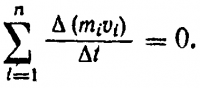
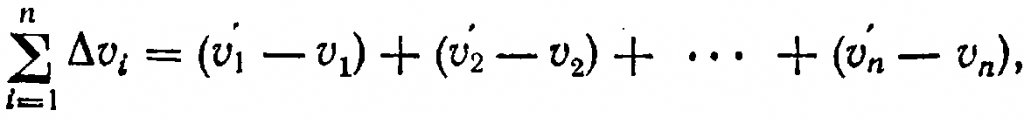
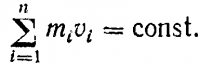
Добавить комментарий
Для отправки комментария вам необходимо авторизоваться.