Центр тяжести (пример как определить)

Центр тяжести это точка внутри тела (или вне его), относительно которой сумма моментов сил тяжести, действующих на отдельные части тела, равна нулю.

Что такое центр тяжести тела

Отыскание центра тяжести тела сводится к нахождению точки приложения равнодействующей параллельных сил тяжести, действующих на отдельные части тела.

Если простейшие геометрические фигуры и тела (например, треугольник, прямоугольник, круг, шар и т. д.) изготовлены из однородного материала, то определить положение центра тяжести можно путем логических рассуждений.

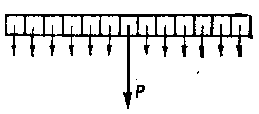
Например, следует определить центр тяжести тонкой однородной прямоугольной пластинки (рис. ). Разобьем пластинку на множество маленьких прямоугольников, равных по величине (и по весу), так как пластинка однородна.

Силы тяжести, действующие на отдельные прямоугольники, направлены параллельно друг другу, как бы пластинка ни была paсположена. Попарно сложим равные параллельные симметрично расположенные относительно центра пластинки силы.

Для каждой такой пары частная равнодействующая приложена к центру пластинки.

Следовательно, равнодействующая всех параллельных сил, действующих на отдельные части пластинки, приложена к ее центру,

Пример решения задач центра тяжести

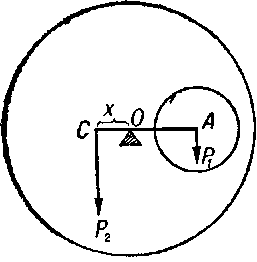
1. В однородном диске радиуса R вырезано отверстие радиуса r < (R/2). Центр отверстия расположен на расстоянии — от центра диска. Определить центр тяжести диска с отверстием.

Решение. Из свойств симметрии очевидно, что центр тяжести диска с отверстием (точка С на рис.41) лежит на продолжении прямой АО, соединяющей центр сплошного диска О с центром выреза А.

Вставив на место ранее вырезанный круг радиусом г, будем рассматривать сплошной диск в виде двух тел с общим центром тяжести в точке О. Сила тяжести малого круга Р₁ приложена в точке А, а сила тяжести Р₂ оставшейся часто,— в точке С. Поместим в точку О ось вращения этой системы тел,

Исходя из равенства моментов сил P₁ и Р₂ относительно этой оси, можно написать соотношение:

P₁ • OA = P₂ • ОС,

где искомое расстояние СО = х, a OA = (R/2) . Но Р₁= m₁g, а Р₂ = m₂g. Массы можно представить таким образом: т₁ = πr²σ, а m₂ = (πR² — πr²) σ, где σ — масса единицы площади диска.

Тогда равенство (1) можно записать так:

πr²σ(R/2) = π(R² — r₂) σx.

Отсюда

x = r₂R/(2(R² — r²)

Пример центр тяжести на наклонной плоскости

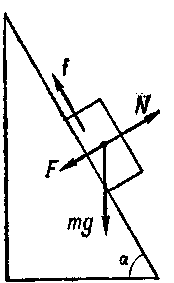
На наклонной плоскости (α = 60°) лежит деревянный брусок массой 3 кг. Какую минимальную силу F следует приложить перпендикулярно к плоскости, чтобы брусок не соскользнул? Коэффициент трения бруска о плоскость k = 0,3.

Дано т = 3 кг, α = 60°, k = 0,3.

F — ?

Решение

На рис. 42 изображены силы, действующие на брусок: f— сила трения, mg — сила тяжести бруска, F — прижимающая сила и N — сила реакции опоры.

Чтобы брусок находился в покое на плоскости, необходимо, чтобы сила трения была больше или по крайней мере равна силе скатывания F_скат ≤ F_тр. 

Как известно, сила скатывания F_скат = mgsinα, а сила трения зависит от коэффициента трения к и от силы нормального давления, которая в данном случае равна F_д = mgcos α + F. 

Значит, f = k (mg cos α + F). Исходя из условия равновесия, можно теперь написать mg sin α ≤ k (mg cos α + F).

Тогда

F ≥ (mg sin α — kmg cos α)/k ≥ (mg/k)(sinα — kcos α),

F ≥ (3кг • 9,8(м/с²))/0,3(sin60° — 0,3 cos60°) ≥ 68,6H.

Статья на тему Центр тяжести