Максимум и минимум функций

  Теория:

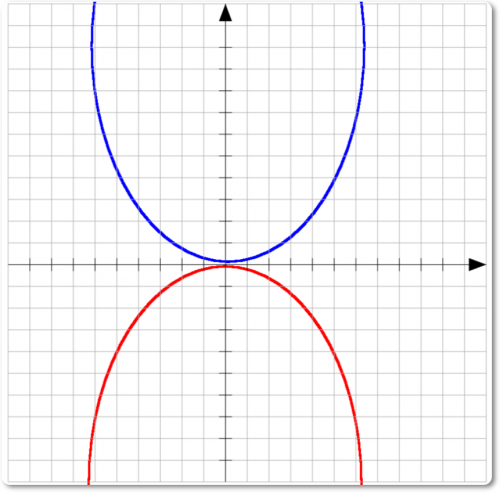
Функция ax² + bx + c выражает собою параболу с вершиной, обращенной книзу, в том случае, когда коэффициент при х — положительный.

При этом точка вершины соответствует наименьшему значению функции.

Если коэффициент при х² — отрицательный, кривая перевернута и ее вершина обращена кверху.

В этом случае функция имеет максимум.

Если мы найдем ось параболы, соответствующую абсциссе — b/2a, то этим определяется максимум или минимум функции, вершина графика которой расположена на указанной оси.

  Практика:

Пример решения

Пример № 1

у = х² — 24х + 108.

Вершина графика выражает минимум, так как коэффициент при х² равен +1.

Абсцисса вершины есть —b/2a, т. е.

— (-24 / 2) = 12.

Следовательно, функция х² — 24х + 108 имеет наименьшее значение при х = 12.

Пример №2

Нужно обнести забором прямоугольный участок земли с трех сторон, с четвертой стороны он ограничен уже имеющейся прямолинейной стеной.

Каковы должны быть размеры прямоугольника, чтобы забор длиною в 4 км отгораживал наибольшую площадь?

Можно построить бесконечное число прямоугольников, сумма сторон которых имеет одну и туже длину, но среди них будет только один такой, который будет заключать максимум площади.

Рассматриваемая нами здесь функция есть площадь прямоугольника, т. е. функция его двух сторон.

Так как нам нужно иметь функцию только от одной переменной, то мы должны выразить одну какую-либо из переменных через другую.

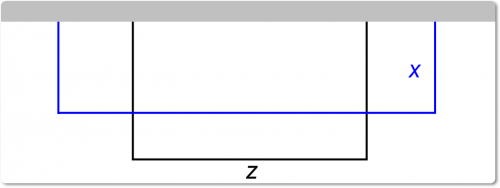
Пусть стороны прямоугольника будут х и z (рис. выше). Так как данная длина забора равна 4 км, то

2х + z = 4

Отгороженная площадь у = х • z; если подставить 4 — 2х в это выражение вместо z, то получим

у = х (4 — 2х) = — 2х² + 4х.

Знак коэффициента при х² — отрицательный, а поэтому функция у будет иметь наибольшее значение при х = -(b/2a) = — (4/ -4) = 1, ибо а = — 2 и b = 4.

2х + z = 4;

2 + z = 4

или

z = 2.

Размеры прямоугольника таковы: 1 км на 2 км.

Площадь прямоугольника равна 2 кв. км.