Теория:
Логарифмическая линейка это устройство для выполнения аналоговых расчетов, которое может осуществлять множество математических операций.
Например умножение и деление, а также возводить числа в степень (чаще всего в квадрат или куб) и извлекать квадратные и кубические корни.
С помощью ее можно вычислять логарифмы, выполнять операции потенцирования и рассчитывать тригонометрические и гиперболические функции, помимо ряда других математических вычислений.
Хотя инженеры пользуются логарифмической линейкой чаще, чем лица каких-либо других профессий, мы все же полагаем, что большинство из них ограничивается выполнением на ней лишь простейших действий.
Когда они сталкиваются с многочисленными правилами пользования линейкой, излагаемыми в соответствующих пособиях, то предпочитают вместо их запоминания применять таблицы логарифмов.
Большинство указанных правил не нужно запоминать, а достаточно ознакомиться лишь с некоторыми основными приемами пользования линейкой.
Логарифмическая линейка по существу представляет собой инструмент, заменяющий таблицу логарифмов.
Линейка состоит из нескольких шкал с нанесенными на них делениями, соответствующими логарифмам чисел.
Отрезки этих шкал могут быть механически сложены или вычтены друг из друга.
С первого взгляда может показаться странным, что выражения, содержащие квадратные и кубические корни, степени чисел, различные тригонометрические функции и т. д..
Могут быть вычислены посредством простого сложения или вычитания отрезков шкал или посредством того и другого действия вместе.
Мы ограничимся рассмотрением логарифмической линейки с различными двойными шкалами, потому что она является наиболее удобной и ее следовало бы иметь каждому инженеру.
Логарифмическая шкала как вычислять
Логарифмическая шкала L. В противоположность обычно принятому порядку, рассмотрим сначала логарифмическую шкалу, обозначенную на американской десятидюймовой счетной линейке буквой L ).
На линейках системы Rietz’a шкала L (логарифмов) находится внизу в виде ординарной шкалы.
Эта шкала называется шкалой равных делений. Как известно, логарифмы чисел, образующих геометрическую прогрессию, сами составляют арифметическую.
Поэтому отсчет следует производить на шкале, разделенной на равные части.
Мантиссы чисел от 1 до 10 нанесены через одинаковые промежутки на протяжении 10 дюймов.
Длина десятидюймовой американской линейки равна 25,4 см.
Она немного разнится от 25 — сантиметровой линейки системы Rietz’a. Устройство шкалы логарифмов одинаково.
Они конечно являются десятичными дробями, как это показано на рис. 1 часть.
Отрезок между каждыми двумя соседними числами разделен на 10 равных частей, которые в свою очередь разделены на пять.
Таким образом эта шкала будет соответствовать трехзначной логарифмической таблице.
При помощи циркуля мы можем измерить на ней два отрезка, например отрезок в 2 дюйма, который соответствует мантиссе 0,2, и отрезок в 3 дюйма, соответствующий мантиссе 0,3, а затем можем сложить эти отрезки.
В результате такого сложения получим отрезок длиной в 5 дюймов, который соответствует мантиссе 0,5, так как шкала разделена на равные части.
Обратимся теперь к рассмотрению шкалы D или таблицы логарифмов. Там мы найдем числа, логарифмы которых суть 0,2, 0,3 и 0,5.
Таким образом имеем:
lg 1,58 + lg 2,01 = lg 3,18
или
1,58 X 2,01 = 3,18.
Рассмотренная шкала является основной шкалой линейки, причем за единицу ее принят отрезок длиной в 10 дюймов.
Каждое из делений 0,100, 0,200, 0,300 и т. д. отстоит от соседнего на 1 дюйм, т. е.
0,100 х 10 = 1,00, 0,200 X 10 = 2,00,
0,300 X 10 = 3,00, и т. д.
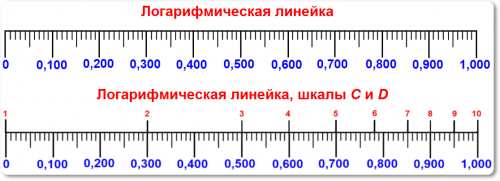
Логарифмические шкалы С и D
Шкалы С и D градуированы по логарифмической шкале L, но вместо логарифмов на них нанесены числа, соответствующие этим логарифмам.
Шкалы С и D американской линейки тождественны по устройству с нижней двойной шкалой линейки системы Rietz’a.
Числа, нанесенные на линейке, и их логарифмы приведены в следующей таблице:
Числа — Логарифмы 1 (0), 2 (0,301), 3 (0,477), 4 (0,602), 5 (0,699), 6 (0,778), 7 (0,845), 8 (0,903), 9 (0,954), 10 (1).
Пример решения:
Сравним логарифмы, нанесенные на шкале L, с числами на шкале D (рис. 2 часть).
Преимущество нанесения на шкалу чисел вместо их логарифмов заключается в том, что при этом нет необходимости рис. 2 часть.
Отыскивать числа в таблице, а их можно читать непосредственно.
При помощи циркуля можно сложить отрезок, соответствующий числу 2, с отрезком, соответствующим числу 3 (на шкале D).
Полученный в результате отрезок отвечает числу 6.
Движок линейки позволяет складывать и вычитать подобные отрезки, что заменяет умножение и деление чисел, соответствующих определенным логарифмам, представленных отрезками.