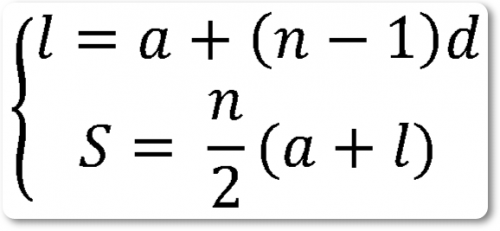Теория:
Арифметической прогрессией называется ряд, каждый член которого, за исключением первого, получается из предыдущего путем прибавления к нему постоянного количества.
Это количество называется разностью прогрессии.
а, (a + d), (a + 2d), (a + 3d), … .
В этой арифметической прогрессии а — первый член, d — разность.
Если а = 3, a d = 4, то прогрессия будет иметь вид:
3, 7, 11, 15, 19, … .
и является возрастающей … ,
Если а = 17 и d = — 7, то получим прогрессию:
17, 10, 3, -4, -11, которая является убывающей.
Так как для получения каждого последующего члена к предыдущему прибавляется постоянная величина d, то для получения третьего члена к а прибавляется 2d, для получения четвертого члена к а прибавляется 3d, для получения n-ного члена к а следует прибавить (n — 1) d.
Отсюда [70] последний n-ный член равен а + (n — 1)d.
В дальнейшем мы будем обозначать последний член буквой l.
Пример решения:
Пример № 1.
Сумма первых членов арифметической прогрессии
Сумма S первых n членов арифметической прогрессии.
Пусть:
S = a + (a + d) + (a + 2d) + … + (l — d) + l.
Напишем члены в обратном порядке:
S = l + (l — d) + … + (а + 2d) + (а + d) + a.
Складывая, имеем:
2S = (a + l) + (a + l) + (a + l) + … + (a + l)
или
2S = n (a + l).
Пример № 2.
Из предыдущего примера имеем:
S = (n/2)(a + l)
где n — порядковый номер последнего члена l.
Так как l = a +(n — 1) d, то, подставляя, получи,
S = (n/2){a + [a + (n — 1) d]}
или
S = (n/2)[2a + (n — 1)d] .
Пример № 3.
Пять величин на арифметическую прогрессию
В большинстве задачах входят пять величин:
a, d, n, l и S.
Если три из них заданы, то остальные две могут был найдены путем решения системы уравнений:
Для удобства представим ряд в следующем виде:
a + (a + d) + (a + 2d) + … + [a + (n — 1) d] = (n/2)[2a + (n — 1) d]
Если три величины составляют арифметическую прогрессию, то член, стоящий между двумя остальными, называется средним арифметическим.
Пусть имеется ряд а, x, b.
Так как разность этих величин одинакова, то:
x — a = b — x.
Решая уравнение, получим:
x = (a + b)/2,
где х есть арифметическое среднее между а и b.