Теория:
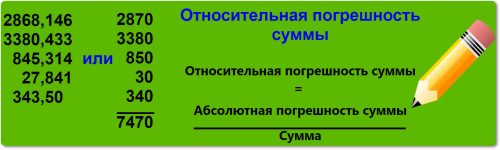
Относительная погрешность суммы нескольких чисел равна абсолютной погрешности суммы, деленной на эту сумму, то есть:
Относительная погрешность суммы = Абсолютная погрешность суммы : Сумма
откуда:
Абсолютная погрешность суммы = Относительной погрешности суммы X Сумму.
Как найти относительную погрешность суммы
Предельная абсолютная погрешность каждого слагаемого не должна быть больше, чем предельная абсолютная погрешность суммы число слагаемых.
К сожалению, в начале сложения сумма еще неизвестна; однако путем грубого приближения можно найти приблизительное значение предельной абсолютной погрешности, которая не должна быть превзойдена в каждом из слагаемых.
Обычно, для получения приближенной величины суммы можно отбросить все цифры, кроме первых, причем при сложении больших и малых чисел последними можно пренебречь.
После небольшой практики получаются очень хорошие результаты.
Практика:
Пример решения относительной погрешности суммы
Найти приближенное значение суммы данных ниже чисел с погрешностью, не превышающей 1% истинной величины этой суммы.
Можно с первого же взгляда сказать, что сумма близка к 7000.
2868,146 + 3580,433 + 845,314 + 343,50 + 27,841
Отсюда: 7000 : 5 = 1400
Умножение на 0,01 дает 14.
Это и есть предельная абсолютная погрешность каждого слагаемого.
Если отбросить единицы, то сумма будет иметь погрешность меньше 1% так как абсолютная ошибка каждого слагаемого меньше 14.
Выполнение действия показано слева, однако при вычислениях не нужно переписывать слагаемые.
Лучше всего при сложении десятков производить округление в уме.
2870 + 3380 + 850 + 30 + 340 = 7470