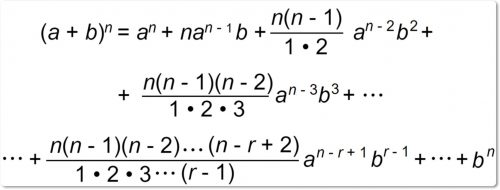Формула бинома Ньютона

  Теория:

Формула бинома Ньютона для целого положительного показателя

Эта формула служит дли разложения (а + b)ⁿ.

Простым перемножением можно, например, найти:

(а + b)² = a² + 2ab + b²

(а + b)³ = a³ + 3a²b + 3ab² + b³

(а + b)⁴ = a⁴ + 4a³b + 6a²b² + 4ab³ + b⁴

(а + b)⁵ = a⁵ + 5a⁴b + 10a³b² + 10a²b³ + 5ab⁴ + b⁵

Если через n обозначить показатель степени, в которую возвышается бином в приведенных выше случаях, то результат можно представить в общем виде таким образом:

Члены этого выражения изменяются по определенному закону, а именно:

1. Показатель буквы а в первом члене разложения ранен показателю степени бинома (в левой части равенства) и уменьшается на единицу в каждом последующем члене. В последнем члене он равен нулю.
2. Показатель буквы b увеличивается на единицу в каждом последующем члене. Будучи нулем в первом члене, он достигает в последнем той же величины, что и показатель степени бинома.
3. Для нахождения коэффициента любого члена, следует умножить коэффициент предыдущего на показатель в нем буквы а и разделить произведение на число предшествующих членов.
4. Если а и b положительны, то перед каждым членом разложения стоит знак плюс, если же b отрицательно, то четные члены (т. е. второй, четвертый и т. д.) будут иметь знак минус.
5. Справедливость такого разложения для целых положительных показателей может быть легко доказана и в общем виде.

Формула бинома для n дробного и отрицательного дана в n° 458.

  Практика:

Пример решения по формуле бинома Ньютона

Удобный способ разложения по формуле бинома заключается в следующем:

Сперва пишут буквы с соответствующими показателями. Под ними помещают коэффициенты каждого члена, а затем их знаки.

Наконец полученные члены соединяют вместе.

Пример. Найти, посредством формулы бинома, пятую степень выражения (b — у).

Имеем:

(b — у)⁵ =

Буквы с показателями	b5	b4y	b3y2	b2y3	by4	y5
Коэффициенты	1	5	10	10	5	1
Знаки	+	—	+	—	+	—
Ответ	b5 — 5b4y + 10b3y2 — 10b2y3 + 5by4 — y5

Примечание. Коэффициент четвертого члена получается умножением коэффициента третьего члена па показатель буквы b, т. е. 10 • 3 = 30, и делением на 3 — порядковый номер этого члена (или число членов, предшествовавших четвертому).