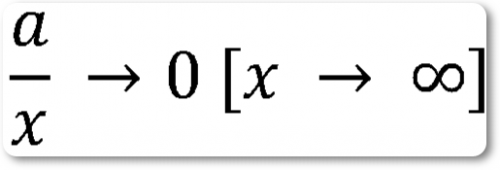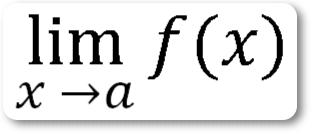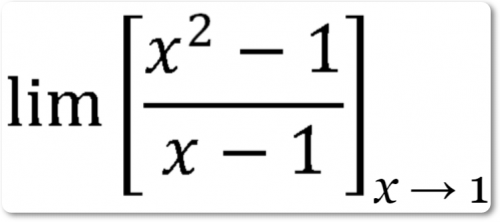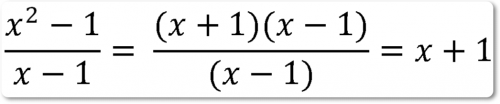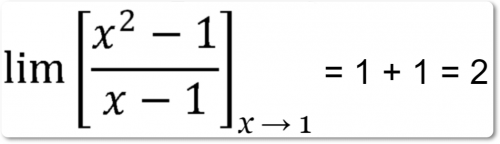Предел переменной (функции)

 Теория:

Пусть переменная принимает ряд значений, которые приближаются к некоторому постоянному числу.

Так что разность между нею и указанным постоянным, начиная с некоторого значения, может быть сделана и остается меньше любого как угодно малого наперед заданного числа.

В таком случае постоянное число называется пределом переменной.

Говорят, что последняя стремится к этому постоянному как к пределу.

Свойства пределов переменных

Переменная 0,3, 0,33, 0,333 . . . , увеличение которой при переходе от предыдущего значения к последующему составляет ¹/₁₀ предыдущего приращения, приближается к 1/3 как к пределу.

0,3 отличается от 1/3 меньше чем на 1/10.

0,33 отличается от 1/3 меньше чем на 1/100.

0,333 отличается от 1/3 меньше чем на 1/1000

Взяв достаточное число десятичных знаков, можно сделать разность между переменной и 1/3 меньше какого угодно малого числа.

Это значит, что разность приближается к пределу нуль, т. е. является величиной бесконечно малой.

Переменная величина

Переменная величина может принимать ряд значений, как например 6,6, 6,66, 6,666 и т. д., приближающихся к некоторому числу, которое не является ее пределом.

В данном случае можно сказать, что значение переменной приближается к 7.

Последнее число однако не является пределом этой переменной, так как невозможно сделать разность между ней и 7 меньше любого малого числа.

Указанная разность всегда остается большей чем 1/3 независимо от взятого числа десятичных знаков. Предел рассматриваемого переменного равен 6²/₃.

Переменная может приближаться к пределу и всегда оставаться больше него или всегда оставаться меньше него, или же быть то меньше, то больше предела.

Во всех этих случаях важно только то, что разность между переменной и ее пределом становится и остается по абсолютной величине меньше любого, как угодно малого, заранее заданного числа.

Переменная величина может изменяться так, что, начиная с некоторого значения, она остается по абсолютной величине все время больше или все время меньше наперед заданного числа.

Если она остается больше любой заданной величины, то говорят, что она обращается в бесконечность или возрастает неограниченно.

То обстоятельство, что переменная х возрастает неограниченно и обращается в бесконечность, обозначается знаком:

х → ∞

Если переменная остается, по абсолютной величине меньше любого наперед заданного числа, то говорят, что она приближается к пределу нуль, и называют ее бесконечно малой.

Это изображаемся знаком х → 0.

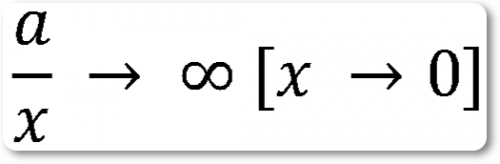
Если постоянное конечное число разделить на бесконечно малую, то частное обращается в бесконечность.

Действительно, если числитель дроби a/x постоянная, а знаменатель уменьшается так, что делается по абсолютной величине меньше любого заранее заданного числа, то частное возрастает и может достичь сколь угодно больших значений.

Если разделить постоянную конечную величину на переменную, которая безгранично возрастает, то частное частное будет числом бесконечно малым.

В самом деле, если числитель дроби a/x есть величина постоянная, а значит стремиться к бесконечности, то частное уменьшается и приближается в пределе к нулю.

Некоторые определения

1. Переменная не может приближаться к двум неравным пределам одновременно.
2. Если две переменные всегда равны между собой и каждая из них приближается к пределу, то их пределы также равны между собой.
3. Предел алгебраической суммы постоянной и переменной величин равен алгебраической сумме постоянной и предела указанной переменной.
4. Предел произведения переменной и постоянной величин равен произведению постоянной на предел переменной.
5. Предел переменной суммы конечного числа переменных равен сумме их пределов.
6. Предел произведения двух или нескольких переменных равен произведению их пределов.
7. Предел частного двух переменных равен частному их пределов (если предел делителя не равен нулю).

Выражение

читается:

(Предел функции х, если х приближается к пределу, равному а).

Если в функции:
4х — 3у
предел х = 5, а предел у = 2, то предел функции от х и у равен:

4 • 5 — 3 • 2 = 14.

 Пример решения:

Найдем

Если подставить значение предела непосредственно в выражение для функции, то получим:

(1 — 1)/(1 — 1) = 0

которое представляется неопределенным.

Разложив предварительно числитель на множители, получим:

так как x →, то 

Данное выражение стремиться к 2 как к пределу, если х приближается к 1.