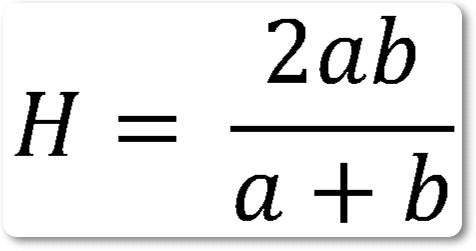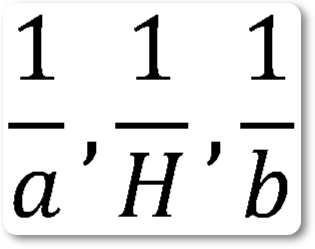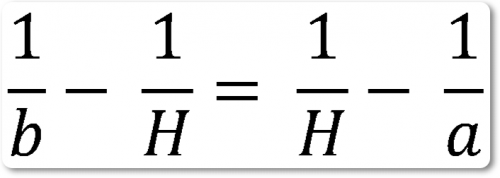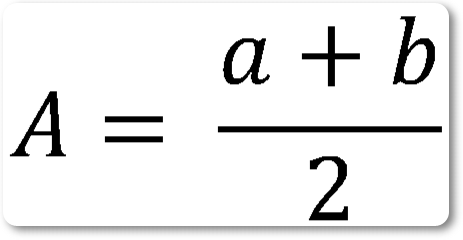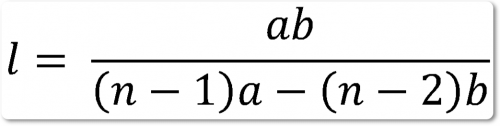Теория:
Гармоническое среднее между двумя числами равно удвоенному произведению этих чисел, деленному на их сумму:
Пусть а и b — два заданных числа, Н — их гармоническое среднее.
По определению, имеем:
откуда
aH — ab = ab — bH
aH + bH = 2ab
или
То есть ее формулу можно прописать так:
H = (2ab)/(a + b)
Среднее геометрическое между двумя числами
Среднее геометрическое между двумя числами есть в то же время геометрическое среднее между их арифметическим и гармоническим средними:
Умножая (1) на (3), получим:
АН = аb.
Извлекая квадратный корень, имеем:
√(AH) = √(ab)
Но G = √(ab) [из (2)], следовательно:
G = √(AH),
т. е. равно геометрическому среднему между арифметическим и гармоническим средними чисел а и b.
Если а и b — первый и второй члены гармонического ряда, то n-ый член этого ряда имеет вид:
Всякий ряд, члены которого образованы по этому закону, есть гармонический.
Пример решения:
Машина едет с пункта a в пункт b со скоростью 80 km/ч. А обратно с пункта b в пункт a со скоростью 90 km/ч.
Найти среднюю среднюю гармоническую скорость.
Используем формулу рис. 1:
H = (2ab)/(a + b)
То есть:
Н = (2 • 90 • 80) : (90 + 80) = 14400 : 170 = 84,7058823529
Ответ: средняя скорость оказалась средним гармоническим двух скоростей которая примерно ≈ 84,7.