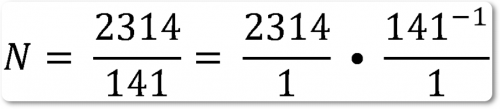Теория:
Деление логарифмов. Вычитаем логарифм делителя из логарифма делимого, получим логарифм частного.
По найденному логарифму найдем из таблиц и самое частное.
Рассмотрим в качестве примера нахождение частного в следующем случае:
lg N = lg 2314 — lg 141
lg N = 3,3643 — 2,1492 = 1,2151.
Из таблиц находим N = 16,41.
Пример:
N = 3,128/0,000168
lg 3,128 = 0,4953
lg 0,000168 = 0,2253 — 4
lg N= 0,2700 + 4
N = 18620.
Если из меньшей мантиссы приходится вычитать большую, то во избежание получения отрицательной мантиссы прибавляем к меньшей единицу и вычитаем эту единицу из характеристики.
Пример решения:
Например:
N = 0,0333 / 49,1
lg 0,0333 = 0,5224 — 2 = 1,5224 — 3
lg 49,1 = 0,6911 + 1.
Теперь можно произвести вычитание:
lg 0,0333 = 1,5224 — 3
lg 49,1 = 0,6911 + 1
lg N = 0,8213 — 4
N = 6,62 • 10-4 = 0,000662.
Число N, соответствующее данному логарифму, называется антилогарифмом последнего.