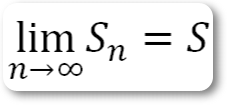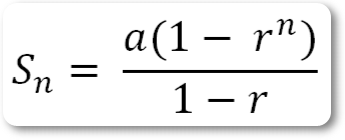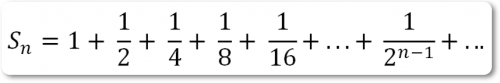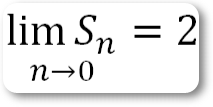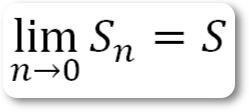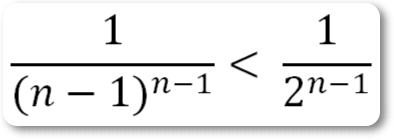Бесконечные ряды (пример решения)

Содержание страницы

Теория:

Бесконечные ряды. Ряд есть совокупность членов, образованных по определенному закону. Рассмотрим ряды, где число членов неограниченно.

Такие ряды называются бесконечными.

Сумма n членов геометрической прогрессии S_n приближается к предельному значению, если r —знаменатель прогрессии — по численной величине меньше единицы и число членов неограниченно возрастает.

Таким образом, взяв достаточно большое число членов геометрической прогрессии, можно сделать разность между их суммой S_n и ее предельным значением как угодно малой.

В случае арифметической прогрессии, как это также было показано, такого предельного значения для суммы ее членов S_n не существует, и по мере возрастания числа членов последняя может возрастать или убывать беспредельно.

Совокупность положительных отрицательных рядов

Если u_1, u₂, u₃.. . . представляют собой совокупность положительных, отрицательных или вместе тех и других количеств, образующих ряд:

u₁ + u₂ + u₃ + . . . + u_n + u_{n + 1} + . . .,

то мы обозначаем сумму первых n членов символом S_n:

S_n = u₁ + u₂ + u₃ + . . . + u_n

Если n возрастает беспредельно, то могут быть два случая:

Случай 1. S_n приближается к конечной величине как к пределу.
Случай 2. S_n к пределу не приближается.

В первом случае мы будем обозначать предел, к которому стремится S_n, буквой S, или символически:

и будем называть такой ряд сходящимся. Этот вид рядов наиболее часто встречается в практических приложениях.

Расходящиеся ряды

Расходящиеся ряды. Во втором случае ряд называется расходящимся.

Здесь можно различать два класса рядов:

Расходящимися рядами являются такие ряды, в которых абсолютная величина S_n по мере увеличения числа членов безгранично возрастает.
Расходящимися являются также ряды, в которых S_n не обращается в бесконечность при увеличении n, но и не стремится к определенному пределу. Такие ряды называются колеблющимися.

Величина S_n колеблется, например, в случае ряда:

S_n = 1 — 1 + 1 — 1 + . . . + (-1)^{n -1}.

Здесь S_n равно либо нулю, либо единице в зависимости от того, является ли п четным или нечетным числом.

Пример сходящихся рядов.

Рассмотрим геометрическую прогрессию:

S_n = a + ar + ar² + ar³ + . . . + ar^{n — 1} + . . .

Положим а = 1, r = 1\2, тогда ряд примет вид:

При увеличении n до бесконечности 1/ 2^{n —} ¹ стремится к 0:

S₁ = 1

S₂ = 1 + 1/2 = 3/2

S₃ = 1 + 1/2 + 1/4 = 7/4

S₄ = 1 + 1/2 + 1/4 + 1/8 = 15/8

Очевидно, что по мере возрастания S_n может быть сделано как угодно близким к 2, т. е. оно может отличаться от 2 на сколь угодно малую величину.

Пример расходящихся рядов.

Рассмотрим арифметический ряд:

S_n = 1 + 2 + 3 + 4 + . . . + n = (n/2)(1 + n)

Очевидно, что, при безграничном увеличении п, сумма членов также возрастает безгранично и ряд является расходящимся.

Бесконечный ряд n общим членом

Иногда бесконечный ряд характеризуют n — ым или, как его называют, общим членом.

В ряде:

2/1 + 3/2 + 4/3 + . . . + (n + 1)/n + . . .

общий или n — й член

u_n = (n + 1)/n

Предел суммы первых n членов сходящегося ряда обозначают так:

и называют суммой ряда.

Характер бесконечного ряда

Характер бесконечного ряда не изменится от добавления или удаления конечного числа членов, т. е. ряд останется сходящимся или расходящимся независимо от того, увеличим ли мы или уменьшим число его членов на конечное количество их.

Однако предел, к которому стремится сходящийся ряд вообще говоря, от этого изменится.

Встречаются ряды, для которых нельзя найти сумму их членов так, как мы это делали в случае геометрической прогрессии, и мы не сможем определить численного значения предела.

Однако при действиях над рядами всегда необходимо знать, существует ли вообще у данного ряда сумма.

Для выяснения вопроса, является ли ряд сходящимся, его нужно исследовать, пользуясь следующими теоремами.

Если, при беспредельном возрастании n, S_n постоянно возрастает, оставаясь все время меньше некоторого определенного числа К, то S_n приближается к пределу, величина которого не более К.

Ряды, состоящие только из положительных членов

Ряд, все члены которого — положительные, не может быть колеблющимся.

S_n в таких рядах всегда возрастает, и если можно доказать, что эта сумма всегда меньше некоторого конечного числа, то ряд должен быть сходящимся.

На этом принципе основан следующий способ испытания рядов на сходимость.

Если, при беспредельном возрастании n, S_n постоянно убывает, оставаясь все время больше некоторого определенного числа К, то S_n приближается к пределу, величина которого не меньше К.

Определение сходимости путем сравнения

Пусть ряд:

u₁ + u₂ + u₃ + . . . (1)

состоит только из положительных членов, и мы хотим определить, является ли он сходящимся.

Пусть, кроме того, известно, что ряд:

u₁ + u₂ + u₃ + . . . (2)

является сходящимся.

Тогда, если каждый член (1) меньше соответствующего члена (2), то ряд (1) — сходящийся, причем его сумма не может быть больше суммы ряда (2) пример № 1.

Пример решения:

Пример № 1

Доказать, что ряд:

2 + 1 + (1/2²) + 1/3³ + 1/4⁴ + . . . (1/((n — 1)^{n — 1})) + . . .

сходящийся.

Сравним его с геометрической прогрессией:

2 + 1 + 1/2² + 1/3³ + 1/4⁴ + . . . (1/((n — 1)^{n — 1})) + . . .

Производя сравнение (1) со (2), мы видим, что, начиная с третьего члена, каждый последующий член ряда (1) меньше соответствующего ряда (2).

После сравнения нескольких членов, мы должны сравнить между собой и n-ые члены (1) и (2).

Если n > 3,

В ряде (2) сумма членов, следующих за третьим, не может превысить 1/4, так как ряд стремится к 3(1/2).

Сумма тех же членов в ряде (1) меньше, чем во (2). Поэтому ряд (1) является сходящимся и его сумма меньше 3(1/2) .