ПОЛЕТ ТЕЛ И ОТНОСИТЕЛЬНОЕ ДВИЖЕНИЕ
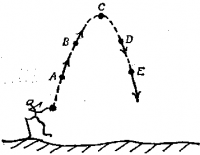
На самом деле летящее тело не совершает отдельно горизонтального и вертикального движения. Когда тело движется по криволинейной траектории, направление его движения в любой момент совпадает с направлением касательной. Поднимаясь от А к В и С (фиг. 34), тело движется все медленнее и медленнее, а затем, падая от С до D и Е, движется все быстрее и быстрее; скорость тела при этом изменяется, поскольку изменяется под действием «земного тяготения» вертикальная составляющая.
Разложение движения по действительной траектории на горизонтальное и вертикальное (т. е. на компоненты) представляет собой искусственный прием, который принимается без доказательств. Каким правилам подчиняется разложение на компоненты, а также обратный процесс сложения компонент?
Процесс сложения отдельных движений в одно движение, которое мы называем результирующим, имеет важное значение в навигации, где приходится складывать движения корабля и океанских течений или движения самолета и ветра. В следующем разделе мы займемся изучением такого сложения движений.
Геометрическое сложение
а) Каким образом разлагается на две составляющие, или компоненты, одно движение по наклонной прямой?
б) Каким образом два отдельных движения складываются в одно движение?
Фиг. 2. Движение летящего тела
Мы можем угадать ответ на второй вопрос и использовать его, чтобы ответить на первый. Если попытаться сложить два или несколько движений, то нам придется следить за передвижением в различных направлениях. Вместо этого пусть движения совершаются в течение некоторого промежутка времени, скажем одного часа, а затем рассмотрим расстояния, пройденные за этот промежуток времени. Тогда задача сложения движений сведется к простой задаче сложения пройденных расстояний или перемещений. Совпадают ли здесь правила сложения с правилом сложения в арифметике, когда, складывая 2 и 3, мы получаем 5?
Рис. 3. Сложение движений, совершаемых в одном и том же направлении.
а — лодка плывет со скоростью 3 км/час; человек идет со скоростью 4 км/час; С — скорость по отношению н берегу 7 км/час.
Если же направления движения оказываются различными, то простая арифметика бессильна. Если к перемещению на 3 м в северном направлении прибавить перемещение на 4 м в восточном направлении, то мы не получим перемещения на 7 м. Точно так же скорость 4 км/час в направлении на восток плюс скорость 3 км/час в направлении на север не даст в сумме скорости 7 км/час в каком-либо направлении. Чтобы действовать в Соответствии с наблюдаемыми в жизни фактами, мы должны пользоваться другим типом сложения, которое мы называем геометрическим сложением.
Здравый смысл (в данном случае простые сведения, приобретенные при ходьбе пешком, вождении автомашин, плавании на лодке и т. д.) подсказывает, как следует производить геометрическое сложение. Предположим, вы хотите сложить перемещения на 4 м к востоку и на 3 м к северу, чтобы найти одно перемещение, которое привело бы вас из исходной точки в пункт назначения. На первый взгляд это кажется несерьезным, но попробуйте проделать это сами.
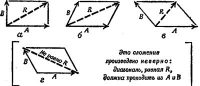
Фиг. 4. Примеры сложения перемещений по правилу параллелограмма
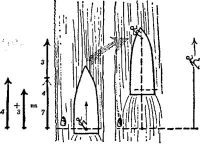
Можно проделать эти перемещения в другом порядке и прийти в тот же пункт назначения. Если бы вы смогли как-то проделать оба перемещения одновременно, то пришли бы в ту же конечную точку. В самом деле, это можно проделать, если приспособить ковер, который передвигался бы по полу при помощи электромотора.
Игрушечный автомобиль движется по ковру, а ковер в это время тянет по полу электродвигатель. Движение автомобиля по отношению к полу совершается по диагонали.
Какое единственное перемещение могло бы заменить эти два, проделанные одновременно или по отдельности, и привести вас в тот же пункт назначения? Простое перемещение по прямой линии из исходной точки в конечную. Это перемещение называют суммой обоих перемещений. Если начертить перемещения в масштабе на бумаге, то однократным перемещением, которое заменило бы оба перемещения (если бы они были сделаны по отдельности), будет перемещение R.
Если перемещения совершаются не под прямым углом, то применимо такое же изображение в масштабе. Если перемещения совершаются одновременно (так бывает, когда полет самолета происходит при наличии ветра) мы можем по-прежнему считать, что сначала происходит одно перемещение, а потом другое, и прийти к результирующему перемещению R.
Мы находим результирующее перемещение, беря сначала одно перемещение, а затем другое.
Объединяя обе эти фигуры, мы видим, что результирующее перемещение дается диагональю параллелограмма, сторонами которого служат первоначальные перемещения.
Это правило для сложения перемещений несомненно верно; в этом нас убеждает здравый смысл, основанный на опыте, приобретенном начиная с раннего детства.
Это правило можно обратить и разложить перемещение R на компоненты А и В. Эти компоненты — одна из возможных пар перемещений, которые вместе дают R. Существует бесконечное множество таких пар, каждая из которых дает в сумме одно и то же перемещение R.
Скорость
Направление перемещения имеет столь же важное значение, как и величина. В физике скорость связывают с определенным направлением. Скорость обладает обоими качествами: величиной и направлением. Подчиняются ли скорости правилу геометрического сложения? Или, как сказал бы ученый, являются ли скорости «векторами»?
Статья на тему Относительное движение


Добавить комментарий
Для отправки комментария вам необходимо авторизоваться.