Линзы это прозрачное тело, которое ограничено двумя криволинейными поверхностями (или одной поверхностью и плоскостью) и по показателю преломления отличается от окружающей среды. В оптических приборах обычно применяются линзы, со сферическими поверхностями. Линзы для видимого излучения изготовляются из стекла, для ультрафиолетового излучения — из кварца, для инфракрасного — из каменной соли или сильвина.
Что такое линзы
Линзами могут являться любые тела, удовлетворяющие данному выше определению, например капельки влаги в воздухе, пузырьки воздуха в воде, круглая стеклянная колба, наполненная водой, и т. п.
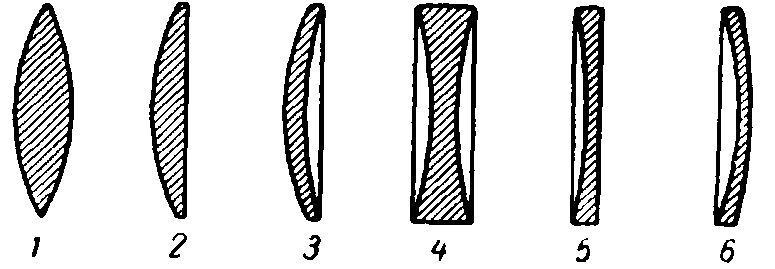
В оптических приборах применяются линзы следующей формы (рис. 2):
- Двояковыпуклая,
- Плоско-выпуклая,
- Вогнуто-выпуклая (радиус выпуклой поверхности меньше, чем радиус вогнутой),
- Двояковогнутая,
- Плоско-вогнутая,
- Выпукло—вогнутая (радиус вогнутой поверхности меньше, чем радиус выпуклой).
Вогнуто-выпуклая и выпукло-вогнутая линзы называются менисковыми и применяются, например в очках.
Оптические свойства линзы можно уяснить, представив сечение ее составленным из трапецеидальных призм, углы наклона граней которых соответствуют кривизне поверхностей, ограничивающих линзу. Центральная часть линзы рассматривается как плоскопараллельная пластинка. Геометрический центр О этой части линзы называется оптическим центром линзы. Прямая ММ , проходящая через центры О1 и О2 кривизны поверхностей, ограничивающих линзу, называется главной осью линзы. Прямая NN , проведенная под любым углом через оптический центр, называется побочной осью линзы. Плоскость РР, проходящая через оптический центр перпендикулярно главной оси, называется главной плоскостью линзы. На этой плоскости обычно и показывают преломление лучей, проходящих через линзу.
Свойства линз

Двояковогнутая (рис. 3, б), плоско-вогнутая и выпукло-вогнутая линзы отклоняют лучи от главной оси. Они называются рассеивающими или отрицательными и обозначаются знаком «—».
Если линза состоит из вещества, показатель преломления которого меньше показателя преломления окружающей среды, то свойства линзы будут обратны указанным; например, пузырек воздуха, ограниченный выпуклыми стенками в воде, действует как рассеивающая линза.
Лучи, падающие на собирающую линзу параллельно главной оси, после преломления пересекутся в точке на оси, называемой главным фокусом линзы (рис. 3, а). Плоскость, проходящая через главный фокус перпендикулярно главной оси, называется фокальной плоскостью линзы. Расстояние главного фокуса от оптического центра называется фокусным расстоянием линзы. Главный фокус со стороны, откуда падает излучение, называется передним с противоположной стороны — задним. Если среда, с которой линза граничит, с обеих сторон одинакова, то одинаковы и фокусные расстояния. Если эта среда различна, то фокусные расстояния также отличаются.
Фокусное расстояние f зависит от радиусов R1 и R2 кривизны поверхностей, ограничивающих линзу, и показателя преломления п вещества линзы относительно окружающей среды. Например, для двояковыпуклой линзы в воздухе
f = 1/(1/R1 + 1/R2)(n -1)
Лучи, параллельные главной оси рассеивающей линзы, отклоняются так, что продолжения этих лучей пересекаются в точке на оси, называемой мнимым главным фокусом линзы (рис. 3, б).
Луч, проходящий линзу вдоль главной оси, не изменяет направления, так как падает перпендикулярно поверхностям линзы. Луч, проходящий вдоль любой побочной оси, преломляется в линзе так же, как в плоскопараллельной пластинке, т. е. несколько смещается, сохраняя прежнее направление. Для тонких линз (так называются линзы, толщина которых значительно меньше наименьшего из радиусов кривизны поверхностей), которые в данном случае рассматриваем, этим смещением за его малостью можно пренебречь и считать, что лучи, направленные вдоль побочных осей, также проходят линзу без изменения направления.
Фокусы лучей, падающих на линзу параллельно побочным осям, лежат в фокальной плоскости линзы. Для того чтобы найти фокус пучка параллельных лучей, падающих на линзу под углом а к главной оси, надо построить под этим углом побочную ось NN, точка F’ пересечения ее с фокальной плоскостью Ф есть фокус данных лучей.
Преломляющая способность линзы характеризуется величиной, которая называется оптической силой линзы. Оптическая сила D линзы измеряется величиной, обратной фокусному расстоянию:
D = 1/f
При этом фокусное расстояние выражается в метрах. Единицей измерения оптической силы является диоптрия (дптр), которая равна оптической силе линзы с фокусным расстоянием 1 м.
У собирающих линз оптическая сила положительна, у рассеивающих отрицательна. Оптическая сила D системы из нескольких сложенных вплотную линз равняется алгебраической сумме (т. е. сумме величин с сохранением их знаков) оптических сил каждой из них в отдельности:
D = ± D1 ± D2 ± … .
Как образуется изображение линзой
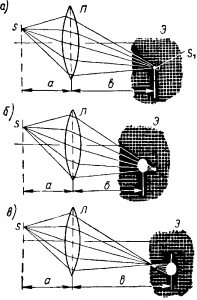
Поэтому для получения резкого изображения экран необходимо располагать строго на определенном расстоянии b от оптического центра линзы, которое находится в определенном соотношении с расстоянием а от оптического центра линзы до плоскости предмета.
В связи с тем что все лучи, исходящие из точки 5 предмета, пересекаются в точке S1 ее изображения, положение последней можно найти как точку пересечения хотя бы только двух лучей, ход которых через линзу известен. Это, во-первых, луч, проходящий через оптический центр, он в тонкой линзе не изменяет свое направление, и, во-вторых, луч, параллельный главной оптической оси, который, преломляясь в линзе, проходит затем через ее главный фокус. Полное изображение предмета затем получается по закону подобия между предметом и изображением.
Рассмотрим некоторые характерные случаи, ограничившись построением для двояковыпуклой линзы.
Точка 5 расположена на главной оси линзы (рис. 5). Проведем из нее какой-нибудь луч SA и параллельно ему побочную ось ВО. Последняя пересечет фокальную плоскость MN в точке С. Через эту точку должен пройти и рассматриваемый луч после преломления в линзе (луч АС). Точка S1 пересечения продолжения этого луча с главной оптической осью линзы и является изображением точки 5.

1/a + 1/b = 1/f
Отношение величины А ‘В’ изображения к величине А В предмета называется линейным увеличением линзы:
k = A’B’/AB.
Из подобия треугольников, а следует, что
k = A’B’/AB = b/a
Линейное увеличение линзы равняется отношению расстояния от плоскости изображения до оптического центра линзы к расстоянию от оптического центра до плоскости предмета.
Применение линз
1. Предмет находится очень далеко от линзы, или, как говорят, в бесконечности, а = ∞; из формулы линзы следует, что b = f и, кроме того, k = b/a = 0, т. е. изображение бесконечно удаленных предметов образуется в фокусе линзы в виде точки.
2. Предмет расположен за двойным фокусным расстоянием линзы:
∞>а > 2f.
Тогда
2f>b>f, и k = b/a <1.
Изображение находится между фокусным и двойным фокусным расстоянием линзы, является действительным, обратным и уменьшенным. Величина изображения тем меньше, чем дальше расположен предмет от линзы. Данный случай имеет место, например, в оптической системе глаза.
3. Предмет находится на двойном фокусном расстоянии:
а = 2f;
тогда b = 2f, следовательно
k = b/a = 1
Изображение действительное, обратное, находится на двойном фокусном расстоянии и имеет такую же величину, как предмет. Линза называется переносной, или оборачивающейся. Такие линзы применяются в качестве вспомогательных в оптических приборах.
4. Предмет расположен между двойным фокусным и фокусным расстоянием линзы: 2f > а > f.
Тогда ∞>b>2fи k = b/a > 1
Изображение действительное, обратное, увеличенное, располагается за двойным фокусным расстоянием. Увеличение изображения тем больше, чем ближе расположен предмет к фокусу линзы. Данный случай встречается, в частности, в микроскопе, где такая линза называется объективом.
5. Предмет расположен на фокусном расстоянии или на расстоянии меньше фокусного:
а ≤ f.
Из формулы линзы получаем: при а = f, b = ∞ при а < f, b — отрицательно.
Если позади такой линзы расположить глаз, то, как увидим ниже, в нем образуется действительное изображение предмета, которое и воспринимается глазом. При этом свойства зрения таковы, что наблюдатель относит это изображение к точкам пересечения продолжения лучей, входящих в глаз (при параллельных лучах изображение относится в бесконечность). В связи с этим геометрическое место точек пересечения продолжения лучей, расходящихся после преломления в линзе, называют мнимым изображением предмета.
Мнимое изображение наблюдается глазом, но может быть получено на экране или фотопластинке, помещенных в плоскости этого изображения.
Линза дает мнимое, прямое, увеличенное изображение.
Подобная линза помещается в приборах всегда около глаза и называется окуляром.
Фокусировка изображения
Если соотношение этих расстояний выдерживается не строго, то изображение получается нерезким (см. рис. 4). В связи с этим во всех оптических приборах имеется приспособление, с помощью которого путем перемещения линзы обеспечивается наводка на резкость изображения, часто неправильно называемая «наводкой на фокус», или «фокусировкой»-изображения.
Если лампа расположена ближе фокусного расстояния линзы, то получить изображение нити на экране не удается.
В оптических приборах применяется также вспомогательная линза, называемая коллективом или собирателем лучей. В необходимых случаях линза изменяет желательным образом ход лучей, не влияя на характер изображения, образуемого основными линзами.
Недостатки линз
Теория построения изображения с помощью линзы рассматривает только узкие световые пучки, которые падают на линзу под небольшим углом к главной оси. В действительности эти условия часто не соблюдаются и тогда изображение, образуемое линзой, имеет ряд недостатков или аберраций.
Основными аберрациями являются:
- Сферическая аберрация, вызываемая широкими световыми пучками,
- Кривизна поля и дисторсия изображения, а также астигматизм, обусловленные падением лучей на линзу под значительным углом к главной оси,
- Хроматическая аберрация, связанная с дисперсией света,
- Астигматизм, обусловленный нарушением сферической формы линзы.
Рассмотрим эти явления применительно к двояковыпуклой линзе. Сферическая аберрация связана с тем, что края линзы, ограниченной сферическими поверхностями, преломляют сильнее, чем центральная часть. Краевые и центральные лучи, параллельные главной оси линзы, после преломления пересекают ось в несколько различных точках F1 и F2, которые и являются для них главными фокусами.
Поэтому изображение предмета, образуемое центральными и краевыми лучами, не лежите одной плоскости. Изображение светящейся точки при этом имеет вид пятна, а изображение протяженных предметов теряет резкость или в центральной или в периферической части. Сферическая аберрация происходит тем сильнее, чем больше кривизна поверхностей, ограничивающих линзу, и чем шире падающие на нее световые пучки.
Кривизна поля изображения заключается в том, что фокусы параллельных лучей, падающих под значительным углом к главной оси линзы, не лежат в фокальной плоскости, но образуют некоторую близкую к ней поверхность. В связи с этим изображение протяженного предмета на плоском экране также имеет различную резкость в центральной и периферической части — результат аналогичный сферической аберрации.
Дисторсия изображения связана с тем, что при значительных углах падения лучей на линзу линейное увеличение для точек предмета, которые находятся ближе или дальше от главной оси линзы, будет отличаться. В связи с этим прямые линии предмета, лежащие в плоскости, перпендикулярной главной оси, в изображении принимают дугообразную форму.
Астигматизм, связанный с наклонным падением лучей, будет рассмотрен позже.
Хроматическая аберрация заключается в том, что вследствие дисперсии лучи с различной длиной волны преломляются в линзе неодинаково и фокусы для них не совпадают. Изображение светящейся точки при этом получается в виде кружка с цветной каемкой. Узкая спектральная каемка появляется и у контуров в изображении предметов.
Для устранения первых трех из указанных аберраций можно с помощью диафрагмы сузить световой пучок, падающий на линзу, но при этом уменьшится яркость изображения.
Более распространенным средством устранения аберраций является сочетание данной линзы с одной или несколькими линзами, которые образуют аберрации обратного характера. Например, сферическая аберрация устраняется путем сочетания с рассеивающей линзой, хотя при этом и уменьшается общая оптическая сила линз.
Хроматическая аберрация устраняется в системе из двух линз из стекла с обратным знаком дисперсии. Это дает компенсацию только по двум цветам — красному и синему. Такая система (в которой скомпенсирована также и сферическая аберрация) называется ахроматом. Для полной компенсации требуется система из большого числа линз. Она называется апохроматом.
Центрированная оптическая система
Оптическая система, которая состоит из нескольких линз, имеющих общую главную ось, называется центрированной оптической системой. Система рассматривается как одно целое и имеет два главных фокуса, две главные плоскости и две узловые точки, которые позволяют построить изображение в такой системе без рассмотрения хода лучей отдельно в каждой линзе.
Главные фокусы F и F’ передний и задний. Это точки, в которых после преломления в оптической системе пересекаются лучи, падающие параллельно главной оси. Фокусные расстояния отсчитываются от главных точек системы.
Главные плоскости системы отличаются тем свойством, что падающий и преломленный лучи пересекают их на одном расстоянии от главной оси (точки М и М’). Главные плоскости перпендикулярны главной оси и пересекают ее в главных точках системы Н — Н’ .
Узловые точки N и N’ системы отличаются тем свойством, что падающий и преломленный лучи проходят через эти точки под одним и тем же углом к главной оси. Если по обе стороны оптической системы находится одинаковая среда (например, воздух), то узловые точки совпадают с главными точками.
Два фокуса, две главные и две узловые точки называются кардинальными точками центрированной оптической системы. Зная . положение этих точек можно использовать для построения изображения центрированной оптической системе те же приемы, как и для одиночной линзы.
Астигматизм линзы
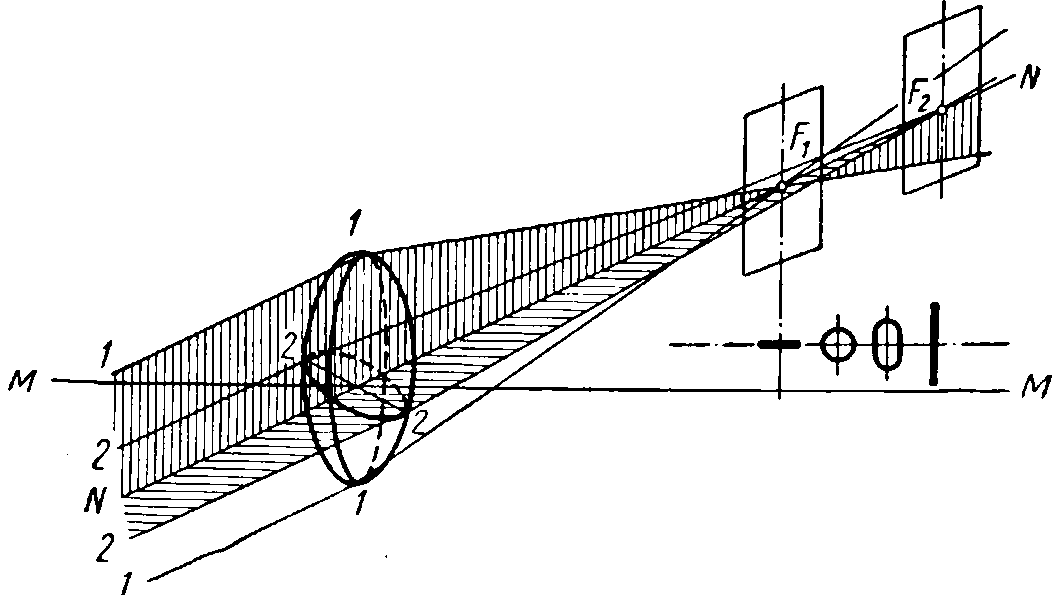
Рассмотрим второй случай. При наиболее простой форме астигматизма неодинаковое преломление лучей происходит в двух плоскостях, соответствующих взаимно перпендикулярным меридианам линзы. Такой астигматизм называется правильным. Допустим, что сферическая линза (рис. 6) с главной осью NN имеет в вертикальной плоскости большую кривизну поверхностей, чем в горизонтальной. Тогда из пучка лучей, падающих параллельно главной оси, лучи 1—1, проходящие по вертикальному диаметру линзы, после преломления пересекутся в точке F1, расположенной ближе, а лучи 2—2, проходящие линзу по горизонтальному диаметру, — в точке F2, расположенной несколько дальше от оптического центра линзы.
На экране, помещенном в точку F1, в которой сходятся лучи 1—1, получится светлая горизонтальная линия, так как лучи 2—2 в этой плоскости еще не пересекаются. На экране, помещенном в точку F2, в которой сходятся лучи 2—2, получится светлая вертикальная линия, так как лучи 1—1 в этой плоскости уже расходятся после пересечения в точке F1. На экране, расположенном между точками F1 и F2, будет светлое пятно, имеющее круглую или овальную форму.
При астигматической линзе изображение светящейся точки имеет вид пятна, вытянутого по определенному направлению, а в изображении предмета контуры, ориентированные в определенных направлениях, теряют резкость.
Крайнюю степень правильного астигматизма имеет линза, ограниченная цилиндрической поверхностью, например плоско-выпуклая цилиндрическая линза. При падении на такую линзу лучей, параллельных главной оси, они будут преломляться только в плоскостях, в которых сечение линзы ограничено криволинейной поверхностью. Лучи 1—1, пересекаясь, после преломления образуют на экране яркую линию АБ. В плоскостях, им перпендикулярных, преломления лучей происходить не будет, так как сечения линзы в этих плоскостях (например, сечение abсd) соответствуют сечениям плоско-параллельной пластинки. Эти лучи на экране создают только равномерно освещенный фон.
При астигматизме наклонных пучков происходит аналогичное явление: лучи, падающие на линзу под большим углом к главной оси, прелом-ляются неравномерно в ее различных меридианных плоскостях, Причем наибольшая неравномерность имеет место также в двух взаимно перпендикулярных плоскостях- Поэтому и результаты будут такие же, т. е. изображение светящейся точки имеет характер пятна, а некоторые контуры предметов теряют резкость. Ход лучей в этом случае можно показать на том же рис. 6, если считать, что линза имеет правильную сферическую форму, но расположена под большим углом к направлению падения лучей. Главная ось линзы для этого случая показана линией ММ.
Астигматизм наклонных пучков можно продемонстрировать, повернув линзу под значительным углом к оси оптической скамьи. При этом в зависимости от положения экрана (несколько ближе или дальше от линзы) будет резким изображение или вертикальных или горизонтальных проволок сетки, т. е. тех проволок, для которых экран находится в сопряженной плоскости.
Для устранения астигматизма наклонных пучков вместе с другими аберрациями применяется система из нескольких соответствующим образом подобранных линз, которая называется анастигматом.
Оптическая диафрагма
Непрозрачное тело (обычно экран) с отверстием, ограничивающее площадь сечения или, как говорят, ширину пучка световых лучей, называется оптической диафрагмой. Отверстие диафрагмы располагается так, чтобы его центр совпадал с главной осью оптической системы, а плоскость отверстия была ей перпендикулярна. Диафрагмой может служить также край или оправа линзы.
Диафрагма, расположенная перед входной линзой прибора, называется апертурной диафрагмой (в общем случае апертурной называется диафрагма, наиболее ограничивающая световой пучок, независимо от места ее расположения в оптической системе).
Апертурная диафрагма Д ограничивает ширину световых пучков, поступающих в систему от отдельных точек предмета, а также не пропускает в систему лучи, которые идут от точек предмета, расположенных на большом расстоянии от главной оси (например, точка N»; от точки N’ лучи проходят, в систему частично). Это способствует устранению аберраций и, следовательно, повышает резкость изображения, но уменьшает его яркость. Апертурная диафрагма также ограничивает поле зрения, т. е. ту часть наблюдаемого предмета, которая дает изображение предмета в оптической системе. Для определения его границ надо провести прямые от точек А пересечения лучей, образующих входной угол б диафрагмы, с диаметром линзы к краям отверстия диафрагмы (линии AN).
Апертурный угол
Угол ϴ, равный половине угла, под которым отверстие апертурной диафрагмы видно из точки пересечения главной оси системы с плоскостью предмета, или, иначе говоря, половина угла, образованного лучами, идущими из этой точки к краям отверстия диафрагмы, называется апертурным углом, или просто апертурой.
Апертурный угол имеет большое значение для разрешающей способности микроскопа. В микроскопе предмет помещается почти у самого переднего фокуса объектива, а апертурный угол ограничивается периметром самой линзы. Поэтому тангенс апертурного угла ϴ равняется отношению радиуса R объектива к его фокусному расстоянию tg ϴ = R/f = D/2f, где D — диаметр объектива. Этой же величине пропорциональна и яркость образуемого объективом изображения.


Добавить комментарий
Для отправки комментария вам необходимо авторизоваться.