Газовые законы

Газовые законы в физике это количественная зависимость между двумя параметрами газа (давление и температура) при фиксированном значении третьего параметра.

Закон Бойля-Мариотта — применим только для идеального газа, это один из основных газовых законов, он описывает изотермические процессы в газе.

Процесс изменения состояния термодинамической системы при постоянной температуре называется изотермическим.

Что такое газовые законы в физике

Газ идеальным, если молекулы его являются материальными точками и, следовательно, он не имеет собственного объема; кроме того, предполагается, что молекулы газа взаимодействуют между собой только в момент столкновения друг с другом.

Из реально существующих газов к идеальному газу приближаются водород и гелий в очень разреженном состоянии.

Состояние вещества определяют такие параметры:

1. Температура,
2. Давление,
3. Объем,
4. Удельная теплоемкость и т. д.

Как определить состояние газа

Для определения состояния газа нет необходимости брать все его параметры. Для этого достаточно выбрать только несколько основных, которые однозначно определяют состояние газа:

1. Давление,
2. Температура,
3. Объем.

Их называют термодинамическими параметрами.

Давление

Если нет внешних воздействий, газ всегда распределяется равномерно по всему заданному объему. Опыт показывает, что газ, заключенный в сосуд, давит на его стенки. Молекулы, двигаясь беспорядочно, ударяются о стенки сосуда. При ударе о стенку на молекулу действует сила, равная изменению импульса молекулы в единицу времени

f = (∆(mυ))/∆t

По третьему закону Ньютона молекула действует на стенку с такой же по величине, но противоположно направленной силой. Учитывая, что на стенку за время ∆t падает N молекул, найдем полную силу

F = — fN = — ((∆(mυ))/∆t)nV

где п —число молекул в единице объема, V —объем, занимаемый газом. Равенство можно переписать так:

F = — nS∆υ(mυ),

где S — площадь стенки.

При упругом ударе молекулы ее скорость меняется на противоположную, то есть υнач = υ, υконеч = —υ, тогда

∆(mυ) = — 2mυ

Окончательно значение силы

F = 2Snmυ²

давление газа на стенки сосуда

р = F/S = 2nmυ²,

где υ —средняя скорость молекул (различные молекулы движутся с (различной скоростью).

Вследствие хаотичности молекулярного движения и огромного числа молекул в единице объема можно утверждать,что в любом направлении движется ¹/₆ часть всех молекул.

Тогда можно показать, что давление газа прямо пропорционально количеству молекул в единице объема и их средней кинетической энергии.

Температура в газах

Температура. Понятие температуры — одно из самых распространенных и в то же время самых сложных физических понятий. Обычно температуру определяют как степень нагретости данного тела.

Но это определение является приближенным, недостаточно строгим.

Температура — это одна из важнейших физических величин, которая определяет состояние тела; ее физический смысл раскрывался постепенно по мере развития физики.

Для измерения температуры обычно выбирают какое-то тело и определяют, как изменяется физическая величина в зависимости от температуры.

Определить различие в тепловом состоянии тел можно с помощью третьего тела, называемого термометром.

Выбор единицы для измерения температуры производится по так называемой шкале температур.

Наиболее распространенной температурной шкалой является шкала Цельсия, в основу которой положено тепловое расширение тел. Она называется термометрической температурной шкалой.

Цельсий для построения своей температурной шкалы взял температурный интервал, заключенный между температурами плавления льда и кипения воды при нормальном атмосферном давлении, и разделил его на 100 равных частей.

Одна сотая этого интервала равна градусу Цельсия.

Термодинамическая шкала

Недостаток термометрической шкалы в том, что зависимость какого-то температурного признака, например, размеров тела от температуры, строго говоря, не бывает линейной.

Кельвин предложил так называемую термодинамическую шкалу, названную абсолютной шкалой Кельвина.

Термодинамическая шкала не зависит от свойств термометрического тела. Она основана на втором начале термодинамики, из которого следует, что отношение теплоты Q₁ полученной телом от нагревателя, к теплоте Q₂, отданной им холодильнику, равно отношению температур нагревателя Т₁ и холодильника Т₂

Q₁/Q₂ = T₁/T₂

Из этого равенства следует, что, зная одну из температур и измеряя отношение можно определить значение неизвестной темпера-туры.

Нуль градусов по этой шкале равен — 273°С (точнее —273,16°С) и называется абсолютным нулем. В шкале Кельвина величина градуса та же, что и в стоградусной шкале Цельсия.

Температура по шкале Кельвина обозначается Т. Температура t° (стоградусной) шкалы Цельсия связана с абсолютной температурой соотношением:

Т = t°+ 273°.

Процессы, протекающие при постоянстве одного параметра и изменении двух других, называются изопроцессами.

Изотермический процесс

Изотермический процесс происходит при постоянной температуре Т = const. Параметры р и V изменяются, оставаясь связанными соотношением

pV = const.

Произведение давления р данной массы газа на объем V при постоянной температуре есть величина постоянная.

Это положение носит название закона Бойля — Mapuomma.

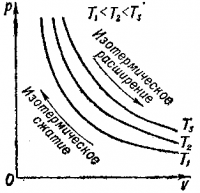
Кривая, изображающая этот процесс при данной температуре, называется изотермой., Чем больше температура, при которой происходит этот процесс, тем выше располагается изотерма (рис. 2).

Изотермический процесс может протекать в двух направлениях, что соответствует изотермическому расширению и изотермическому сжатию газа.

Поскольку температура газа не изменяется, то при расширении газа тепло к нему должно подводиться извне, а при сжатии — тепло должно отдаваться во внешнюю среду.

Закон Бойля для идеального газа

Закон Бойля — Мариотта применим только для идеального газа. Для реальных газов этот закон приблизительно выполняется при малых давлениях и высоких температурах.

Внутренняя энергия U идеального газа равна сумме кинетической энергии W_к молекул.

Внутренняя энергия реального газа равна сумме потенциальной W_п и кинетической W_к энергии всех молекул.

При малых давлениях и высоких температурах взаимодействие между молекулами мало, а кинетическая энергия молекул велика, поэтому потенциальной энергией можно пренебречь, тогда

Uр.газ ≈ ΣW_к.

При давлениях в сотни атмосфер и выше экспериментальные значения произведения pV уже значительно отличаются от теоретических.

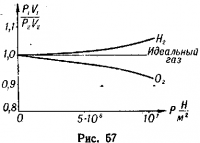
На графике (рис. 3) приведены некоторые данные по сжатию водорода и кислорода при температуре t₀° = 0° С, с начальным давлением р₀ = 10⁵ (H/м²) и одинаковом начальном объеме V₀ = 22,41 л.

Определение изотермического процесса

Можно доказать, что при изотермическом процессе давление газа изменяется прямо пропорционально его плотности.

Пусть при постоянной температуре ρ₁ — плотность газа при объеме V₁ и давлении р₁, а ρ₂ — плотность газа при объеме V₂ и давлении р₂ тогда

ρ₁ = (m/V₁), ρ₂ = (m/V₂).

Разделив эти два равенства почленно и заменив отношение объемов отношением давлений по закону Бойля — Мариотта

V₂/V₁ = p₁/p₂

Изобарический и изохорический процессы

Процесс изменения состояния газа при постоянном давлении называется изобарическим (р = const). Пусть при температуре 0° С объем газа равен V₀, а при температуре t° С — объем V_t, давление при этом постоянно.

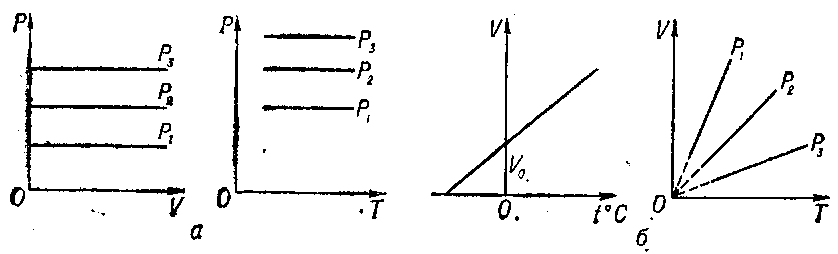
Увеличение объема, приходящегося на каждую единицу объема, взятого при 0° С, при нагревании на один градус

β = (V_t — V₀)/(V₀t°)

откуда

V_t = V₀(1 + βt°)

β — коэффициент объемного расширения газа при постоянном давлении одинаков для всех идеальных газов и равен

β = (1/273)град^-1

Подставив значение β в равенство и сделав преобразование, получим:

V_t = V₀(1 + (t°/273°) = (V₀(273° + t°))/273°. Помня, что Т = 273° + t°, можно записать

V_t = (V₀T)/273°

Если при температуре Т₁ определенное количество газа, расширяясь изобарически, имеет объем V_l, а при температуре Т₂ — объем V₂, то

V₁ = (V₀T₁)/273°, V₂ = (V₀T₂)/273°.

Поделив почленно, получим

V₁/V₂ = T₁/T₂.

Закон Гей-Люссака для изобарического нагревания

Это соотношение получило название закона Гей-Люссака. Из него следует, что объем данной массы газа при изобарическом нагревании прямо пропорционален абсолютной температуре.

Исходя из уравнения закона Гей-Люссака, можно показать, что плотность газа при р = const обратно пропорциональна абсолютной температуре. ИмеV₁/V₂ = T₁/T₂ , но

V₁ = m/ρ₁, V₂ = m/ρ₂,

где V₁ и ρ₁ — объем и плотность при температуре T₁; V₂ и ρ₂ — при температуре Т₂, тогда

mρ₂/mρ₁ = T₁/T₂, или ρ₂/ρ₁ = T₁/T₂.

Графики изобарического процесса в координатных осях р, V и р,Т (рис. 3, а) не требуют пояснения. Графики в осях V, t° и V, Т (рис. 3, б) строятся по уравнениям (1) и (2).

Процесс изменения состояния газа при постоянном объеме называется изохорическим. Зависимость между давлением и температурой при нагревании данной массы газа постоянного объема выражается законом Шарля

p_t = p₀ (1 + γt°),

где p_t — давление при температуре t°; р₀ — давление при 0° С;γ — термический коэффициент давления, показывающий на сколько изменяется каждая единица первоначального давления при изменении температуры от 0° до 1° С.

Для всех газов

γ ≈ (1/273) град^-1.

Рассуждая точно так же, как при анализе уравнения закона Гей-Люссака, можно получить такую форму записи закона Шарля

р₁/р₂ = Т₁/Т₂

Давление данной массы газа при постоянном объеме прямо пропорционально абсолютной температуре.

Графики изохорического процесса аналогичны графикам изобарического процесса.

Физический смысл абсолютного нуля

Из графика изохорического процесса в координатах р, t° видно, что с уменьшением температуры давление падает и при какой-то температуре становится равным нулю.

Определим эту температуру из уравнения

р_t = р₀ (1 + αt°).

Если p_t = 0, то р₀ (1 + αt°) = 0, но р₀ ≠ 0, поэтому 1 + αt°=

= 0, откуда

t° = —(1/α) = —273°С.

Эту температуру, как было сказано выше, назвали абсолютным нулем. Выясним физический смысл абсолютного нуля.

Определение абсолютного нуля

При Т = 0°К давление должно равняться нулю р = 0, но р = (2/3)n₀w_к.ср. или, что то же самое, где п₀ — число молекул в единице объема, w_к.сp — средняя кинетическая энергия молекул, υ_cp — средняя скорость молекул.

Однако п₀ ≠ 0 и m ≠ 0, следовательно, υ_cp = 0, то есть при температуре абсолютного нуля полностью прекращается поступательное движение молекул газа.

Другие виды движения молекул (вращательное и колебательное) могут существовать и при Т = 0°К.

Установлено, что такое состояние вещества недостижимо, но к нему можно подойти очень близко.

Объединенный закон газового состояния

Переход газа из одного состояния в другое может происходить при одновременном изменении параметров р, V, Т.

Будем переводить газ, состояние которого описывается параметрами р₁V₁T₁ в состояние, описываемое параметрами p₂V₂T₂, постепенно, через промежуточное состояние.

Сначала переведем газ изотермически в промежуточное состояние, которое описывается параметрами: 

p₂V’T₁.

Тогда состояние газа можно описать уравнением закона Бойля — Мариотта

р₁V₁ = p₂V’,

где V — объем при температуре T₁ и давлении р₂.

Из промежуточного состояния перейдем в конечное, которое описывалось бы параметрами p₂V₂T₂. Так как давление газа одинаково в обоих состояниях, то можно применить закон Гей-Люссака

V₂/V‘ = T₂/T₁,

отсюда

V‘ = (V₂T₁)/T₂.

Подставив значение V‘ в уравнение, получим: р₁V₁ = p₂V₂(T₁/T₂) или (р₁V₁)/T₁ = (p₂V₂)/T₂.

Это соотношение можно записать и так:

(pV)/T = В.

Получили уравнение газового состояния для данной массы газа: отношение произведения давления на объем к абсолютной температуре есть величина постоянная.

Универсальная газовая постоянная

Численное значение постоянной В зависит от рода газа, его количества и системы единиц, в которых измеряются р, V, Т.

Так как грамм-молекула любого газа при 0° С и нормальном давлении занимает объем V₀ = 22,4 л, то постоянная В, отнесенная к одному молю газа, будет иметь одно и то же значение для любого газа.

Эту общую для всех газов постоянную обозначают R и называют универсальной газовой постоянной. Численное значение универсальной газовой постоянной в СИ равно

R = 8,31 • 10³(Дж/кмоль•град).

Состояние одного моля газа описывается уравнением

pV₀/T = R.

Эту формулу можно обобщить и для любой массы газа.

Если через р обозначить массу киломоля данного газа, а через V₀ занимаемый им объем при данных р и Т, то m граммов газа при тех же давлении и температуре займут объем V = (m/μ) V₀.

В связи с этим и величина отношения pV/T для m граммов газа будет в m/μ раз больше газовой постоянной R, то есть

pV/T = (m/μ)R.

Это уравнение справедливо уже для любой массы любого газа. Обычно его записывают так:

pV = (m/μ) RT.

Данное уравнение называют уравнением Менделеева — Клапейрона.