Определитель в математике
Выражения вида a1b2 — a2b1 где a1, a2b2 , b2 суть какие-нибудь числа, встречаются в математике весьма часто и называются определителями.
Соотношение a1b2 — a2b1 написанное в форме:
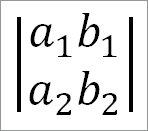
называется определителем второго порядка.
Определитель n-го порядка состоит из n2 элементов, расположенных в n строках и n столбцах.
Так, указанный выше определитель состоит из четырех элементов, расположенных в двух строках и двух столбцах.
Для разложения определителя второго порядка следует вычесть из произведения элементов, лежащих на главной диагонали, произведение элементов, расположенных на другой диагонали.
Например:
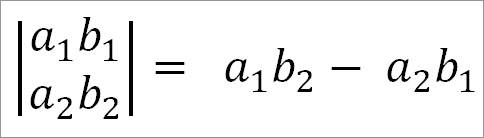
и
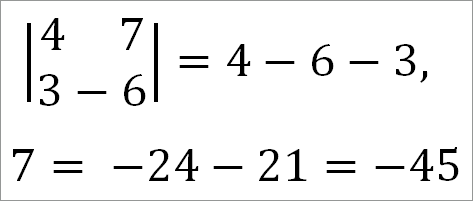
Каждый член разложения содержит только один элемент из каждой строки и один—из каждого столбца.
Система уравнений с двумя неизвестными
а1х + b1y = c1
Решая эти уравнения посредством обычного аналитического метода подстановки, имеем:
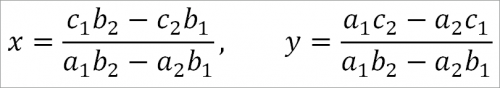
Написав числители и знаменатели в форме определителей, получим:
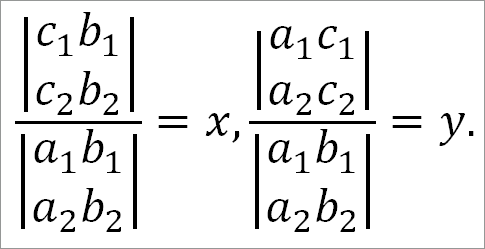
Определители, находящиеся в знаменателях, одинаковы. Они составлены из коэффициентов при х и у в данных уравнениях
Числитель выражения
Каждый определитель, стоящий в числителе, получается из определителя, стоящего в знаменателе, путем замены коэффициентов при искомых неизвестных постоянными членами.
Чтобы найти числитель выражения для х, следует заменить коэффициенты при х (т. е. а1 и а2) постоянными членами с1 и с2.
Точно также для нахождения величины y нужно заменить b1 и членами c1 и с2.
Пример. Решить посредством определителей систему:
2х — y = 1
3х + 2y = 3.
Определитель для знаменателя будет иметь вид:
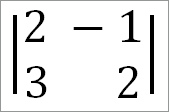
как для х, так и для y.
Для получения числителя дроби в выражении для х следует заменить коэффициенты при х постоянными членами 1 и 3, тогда найдем:
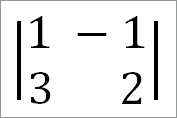
Поэтому
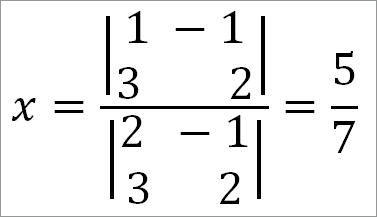
Точно так же найдем
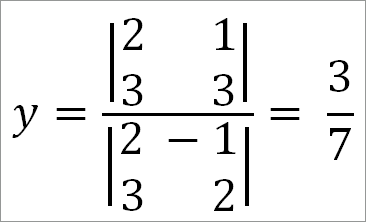
Определитель третьего порядка
Определитель, состоящий из 9 элементов, расположенных в трех строках и трех столбцах, называется определителем третьего порядка.
Так
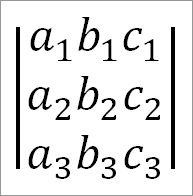
есть определитель третьего порядка.
Он является весьма удобным обозначением выражения:
a1b2c3 + a2b3c1 + a3b1c2 — a1b3c2 — a2b1c3 — a3b2c1.
Заметим, что здесь каждый член представляет собой произведение трех элементов по одному из каждого столбца и по одному из каждой строки.
Написанное выражение может быть преобразовано таким образом:
а1(b2с3 — b3с2) — а2(b1с3 — b3c1) + a2(b1c2 — b2c1).
Члены, заключенные в скобках, являются развернутыми определителями второго порядка, поэтому определитель третьего порядка может быть представлен так:
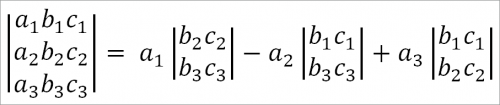
Произведение
Итак, мы установили весьма важный способ получения определителей второго порядка из определителей третьего порядка.
Составим произведение из каждого элемента первого столбца и определителя второго порядка, который получается после вычеркивания того столбца и строки, в которых расположен данный элемент.
Взяв а, отбросим (зачеркнем) первую строку и первый столбец:
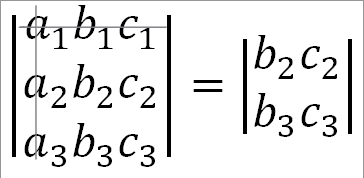
Взяв а2 отбросим вторую строку и первый столбец:
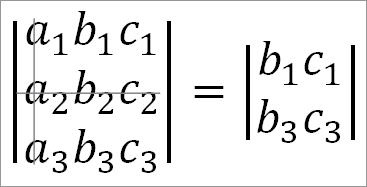
Взяв а3, отбросим третью строку и первый столбец:
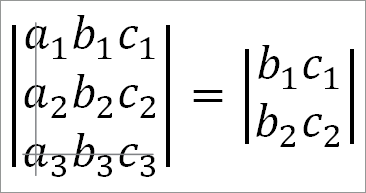
Чтобы получить разложение определителя третьего порядка на определители второго порядка, следует изменить знак второго члена.
То есть произведения элемента, находящегося во второй строке и первом столбце, и соответствующего определителя второго порядка.
Определитель следующего низшего порядка, получающийся путем вычеркивания строки и столбца, в котором стоит известный элемент, называется минором этого элемента.
Так например, в определителе:
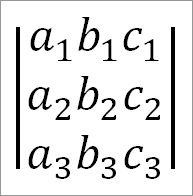
минор члена а1 есть определитель:
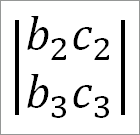
Если минору приписан надлежащий знак, то его называют алгебраическим дополнением соответствующего элемента.
Решение системы трех уравнении первой степени
a1x + b1y + c1z = d1
a2x + b2y + c2z = d2
a3x + b3y + c3z = d3
Предполагая, что коэффициенты при неизвестных, входящие в определители, не равны нулю.
Получим для каждого из этих неизвестных частное двух определителей, точно так же как и в случае системы двух уравнений.
Знаки алгебраических дополнений
Если элемент расположен в р-ой строке и в m-ом столбце, то его минор, умноженный на (-1)m+р, называется алгебраическим дополнением элемента.
Возьмем, например, минор элемента в определителе 4-го порядка:
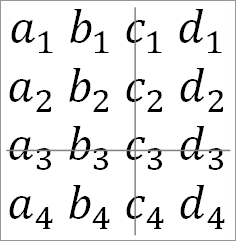
Алгебраическим дополнением с3 будет:
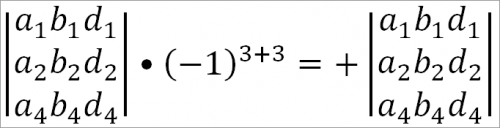
Здесь
m = 3, так как с3 стоит в третьем столбце
р = 3, так как с3 стоит в третьей строке.
Алгебраические дополнения a1, a2, a3 обычно обозначаются буквами: А1, A2, A3 а определитель системы буквой D.
Таким образом
D = a1A1 + a2A2 + a3A3
Определители n-го порядка
Для решения системы п линейных уравнений с n неизвестными, необходимо составить определитель, и который войдут все n3 коэффициентов при неизвестных из заданных уравнений.
В таком случае получим определитель n-го порядка, обозначаемый обыкновенно буквой ∆ (дельта):
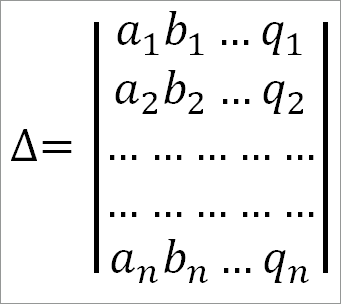
Этот определитель заменяет собой алгебраическую сумму произведений и множителей, каждый из которых может быть получен, если взять один элемент из каждой строки и один элемент из каждого столбца.
Соответственно правилу каждому такому произведению нужно приписать знак плюс или минус в зависимости от его расположения в определителе.
Свойства определителей
Разложение определителя n-го порядка дает n! членов.
- Если все элементы столбца или отроки суть нули, то определитель равен нулю, ибо, разлагая по элементам этого столбца или строки, получим все члены равными нулю.
- Величина определителя не изменится, если заменить строки столбцами или наоборот. Это можно доказать, производя разложение определителя.
- Всякая теорема, справедливая для столбцов определителя, справедлива и для его строк, и обратно.
- Перестановка двух строк или столбцов одного на место другого изменяет знак определителя.
- Если две строки или два столбца определителя одинаковы, то определитель равен нулю.
- Если элементы какого-нибудь столбца (или строки) умножить на алгебраические дополнения соответствующих элементов другого столбца (или строки), то сумма их произведений равняется нулю.
Так например,
b1A1 + b2A2 + b3A3 + . . . + bkAk = 0
a2A1 + b2B1 + c2C1 + . . . + k2K1 = 0
- Только-что доказанная теорема справедлива и для случая деления, так как деление на m равносильно умножению на 1/m
- Если каждый элемент одного из столбцов определителя представить в виде суммы двух количеств, то данный определитель можно заменить суммой двух определителей того же порядка.
- Если умножить каждый элемент столбца (или строки) на одно и то же число и произведение прибавить (или отнять) к соответствующим элементам другого столбца (или строки), то определитель по величине не изменится.
Разложение определителей
Посредством применения принципа, можно обратить все элементы столбца (или строки), кроме одного, в нули, причем порядок определителя может быть понижен на единицу.
Этот процесс можно продолжать до тех пор, пока не получится определитель второго порядка.
Перед понижением порядка определитель во многих случаях можно упростить путем сокращения на множители, общие для всех элементов столбца или строки.
Кроме того можно уменьшить абсолютные величины членов, вычитая соответствующие элементы других столбцов (или строк) или их кратные.
Разложение определителей на множители
Если определитель обращается в нуль при замене какого-нибудь элемента b, другим элементом а, то разность чисел а и b является множителем определителя.
Пример.
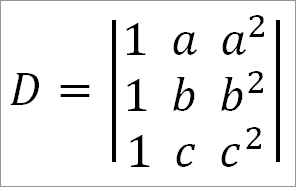
Если а = b, то
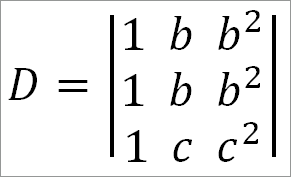
Так как две строки в этом о в ре дели теле одинаковы, то D = 0 и (а — b) является его множителем. По той же причине (b — с) и (с — а) также являются множителями данного определителя.
Произведение этих трех множителей имеет ту же степень и может отличаться от D только коэффициентом k.
Поэтому
D = k(а — b)(b — с)(с — а).
Член, полученный из главной диагонали первоначального определителя, равен bс2.
Он должен быть равен соответствующему члену в выражении k(а — b) (b — с)(с — a) или kbc2
bc2 = kbc2. т. е. k = 1.
Следовательно:
D = (a — b)(b — с) (с — а).


Добавить комментарий
Для отправки комментария вам необходимо авторизоваться.