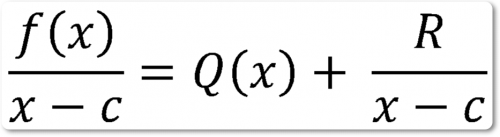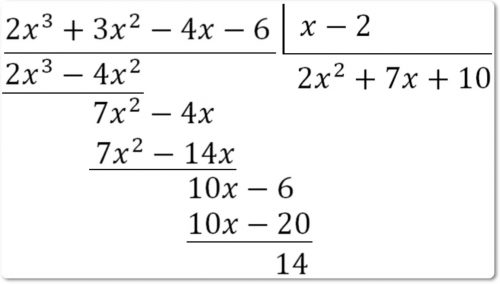Теория:
Теорема. Если многочлен f(x) разделить на х — с, то остаток равен f(с), т, е. величине многочленах в который вместо х подставлено с.
Доказательство. Пусть частное от деления многочлена f(x) на х — с равно Q(х), а остаток равен постоянному R, так что:
Требуется доказать, что:
R = f(c)
Из выражений:
f(x) = a0xn + a1xn-1 + • • • + an-1x + an
f(c) = a0cn + a1cn-1 + • • • + an-1c + an
получаем:
f(x) — f(c) = a0xn + a1xn-1 + • • • an-1x + an — (a0cn + a1cn-1 + • • • + an-1c + an) = a0(xn — cn) + a1(xn-1 — cn-1) + • • • + an-1(x — c)
Так как множитель (х — с) входит во все члены последнего выражения, то можно вынести его за скобки, обозначив оставшееся в скобках выражение через Q(x); тогда получим:
f(x) — f(c) = (x — c) [Q(x)]
Деля на (х — с), найдем:
f(x)/(x — c) = Q(x) + (f(x)/(x — c)), то есть R = f(c),
что и требовалось доказать.
Пример решения:
Пусть f(x) = 2x3 + 3x2 — 4x — 6, a c = 2.
f(c) = 2 • 23 + 3 • 22 — 4 • 2 — 6 = 14 = остатку.