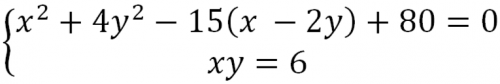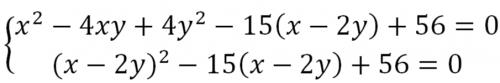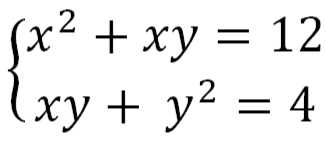Теория:
Решение посредством преобразования уравнений. Многие системы уравнений могут быть легко решены посредством нахождения величины для каждых двух выражений:
x + y, x — y, xy.
а равно и других функций х и у, из которых можно получить значения этих неизвестных.
Практика:
Пример решения преобразованием уравнений
Пример № 1. Найти корни уравнений
Умножая (2) на 4 и вычитая ив (1), имеем:
Решаем сначала относительно функции (х — 2у), а затем относительно х и у.
Пример № 2. Решить систему
Складывая (1) к (2), находим:
х3 + 2xy + y2 = 16.
Вычитая (2) ив (1):
x2 — y2 = 8 (4)
Извлекая квадратный корень из (3):
х + у = ± 4.
Разделив (4) иа (5), находим:
x — y = ± 2
Из (5) и (6):
х = 3 или — 3, у = 1 или — 1.
Первое значение х — у соответствует только первому значению x + у.
Следовательно, для х и у имеется только две пары значений.
Иногда применяются специальные способы решений, при которых сперва находят величины выражений:
√(xy), √(x + y), 1/x, 1/y, xy, (x + y), (x + y)2, x2y и т. д.,
после чего определяют х и у.
В некоторых случаях оказывается удобным вводить новые переменные, например √ (ху) = u и т. д.
Наиболее обычны подстановки:
x = u + υ, у = u — υ, y = υx.