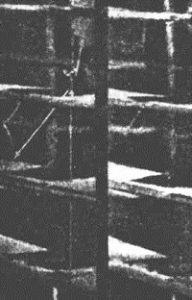
История квантовой статистики
Рис. Явление Комптона по снимку Комптона и Симона
Статья Бозе заинтересовала Эйнштейна, и он сопроводил ее публикацию своим примечанием, помещенным в конце статьи: «Вывод формулы Планка, предложенный Бозе, является, по моему мнению, большим достижением. Использованный им метод дает также квантовую теорию идеального газа, которую я изложу в другом месте».
Число таких распределений выражается формулой:
где
ps0 — число пустых ячеек, ps1 — число ячеек, содержащих один квант, ps2— число ячеек, содержащих два кванта, и т. д. Отсюда Бозе, определяя наиболее вероятное состояние, находит формулу Планка.
Эренфест рассказывал своим друзьям, что, начав читать статью Бозе, он отнесся к ней весьма неодобрительно. Но, прочитав в конце примечание Эйнштейна, он сказал себе: «Пауль, ты чего-то не понял». Эйнштейн же выполнил свое обещание и опубликовал в 1924— 1925 гг. ряд статей по квантовой теории идеального одноатомного газа. Вклад, внесенный Эйнштейном в развитие статистики Бозе, оказался столь существенным, что ныне эту статистику называют статистикой Бозе—Эйнштейна. Из этих статей видно, с каким трудом пробивали дорогу новые идеи. Эйнштейн указывал, что «Эренфест и другие коллеги порицают теорию излучения Бозе и мою теорию идеального газа» и отвечал на критику, уточняя и развивая новую теорию. При этом Эйнштейн, который еще в 1909 г. рассматривал интерференционные флюктуации светового поля, вводит представление о таких флюктуациях и в теорию газа, считая, что «здесь речь идет не только о простой аналогии».
«Каким образом материальной частице или системе материальных частиц можно сопоставить (скалярное) волновое поле, — пишет Эйнштейн,— показал в своей работе Л. де Бройль, заслуживающей всякого внимания». При этом Эйнштейн ссылается на докторскую диссертацию де Бройля.
Эйнштейн был первым из крупных физиков, который поддержал идеи де Бройля и широко использовал их в своих исследованиях по квантовой статистике идеального одноатомного газа.
По-иному отнеслись к теории де Бройля Бор и его сотрудники по «копенгагенской школе ». Бop, Гейзенберг, Паули искали выхода на путях построения математических схем, лишенных наглядности, но зато точно описывающих наблюдаемые факты. Такая математическая схема была найдена в 1925 г. Гейзенбергом.
При этом Гейзенберг, как он отмечал в аннотации к статье «О квантовотеоретическом истолковании кинематических и механических соотношений», основывался «исключительно на соотношениях между принципиально наблюдаемыми величинами». В статье, представленной в редакцию «Zeitschrift fur Physik» 29 июня 1925 г., Гейзенберг предлагал «отказаться от всякой надежды на наблюдение до сих пор не наблюдаемых величин (таких, как положения, период обращения электрона)» и пытался «построить квантово теоретическую механику, более или менее аналогичную классической механике, в которой встречались бы только соотношения между наблюдаемыми величинами».
Нельзя не отметить, что этот призыв Гейзенберга отказаться от «до сих пор не наблюдаемых величин» напоминает призыв Маха и Оствальда «отказаться от не наблюдаемых» атомов и электронов. Гейзенберг еще не сознавал, что речь идет не об отказе от понятия «не наблюдаемые» положения и скорости электрона, а об уточнении самого понятия «наблюдение» в применении к микромиру. Гейзенберг не знал также, что предложенная им в статье математическая схема описания квантовотеорети-ческих величин есть матричная алгебра. На это указал учитель Гейзенберга М. Борн, который вместе с П. Иорданом 27 сентября 1925 г. представил в «Zeitschrift fur Physik» статью о матричной теории гармонического осциллятора.
В октябре того же года В. Паули разработал по новой теории проблему атома водорода. 26 ноября 1925 г. Борн и Иордан представили в «Zeitschrift fur Physik» «общую математическую теорию квантовой механики». В том же 1925 г. П. Дирак выступил со своей схемой новой механики, развив особую символическую алгебру состояний и наблюдаемых величин. При этом существенно, что Дирак, ознакомившись со статьей Гейзенберга еще до ее публикации (Гейзенберг прислал ему препринт), обратил внимание не на методологическую установку Гейзенберга, а на нарушение принципа коммутативности для произведения величин, входящих в описание атомной системы. «Это в самом деле было более важно,— вспоминал позднее Дирак,— чем мысль Гейзенберга о построении теории на основе величин, тесно связанных с результатами экспериментов. Поэтому я, — продолжал Дирак,— сосредоточил свое внимание на мысли о некоммутативности, стремясь понять, как следует изменить обычную динамику, которой до сего времени люди пользовались, чтобы включить эту идею в теорию… Гамильтонова форма динамики оказалась как раз наиболее подходящей формой для включения некоммутативности, и не столь уж трудной задачей было найти способ сочетать эти мысли».
Статья на тему История квантовой статистики

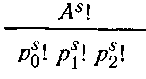
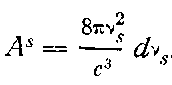
Добавить комментарий
Для отправки комментария вам необходимо авторизоваться.