Колебательное движение это такое периодически повторяющееся перемещение материальной точки, при котором она движется по какой-либо траектории поочередно в двух противоположных направлениях относительно положения наиболее устойчивого равновесия.
Примеры колебательного движения: движение тела, закрепленного между двумя натянутыми пружинами, колебания маятника часов, колебания звучащего камертона и др.
Что такое колебательное движение
Колебания могут происходить как при наличии внешней по отношению к колебательной системе периодической силы (вынужденные колебания), так и под действием сил, действующих внутри самой системы (свободные колебания).
Необходимыми условиями для возникновения и поддержания колебаний материальной точки являются:
- Наличие у колеблющейся точки энергии;
- Действие на материальную точку возвращающей силы;
- Полученная материальной точкой энергия при смещении из положения равновесия не должна полностью расходоваться на преодоление сопротивлений, когда точка возвращается в положение равновесия.
Рассмотрим движение материальной точки массы т под действием упругой пружины. Массой самой пружины будем пренебрегать. Точка О на горизонтальной оси соответствует положению равновесия материальной точки, когда пружина не деформирована (рис. , а).
При смещении точки вправо на величину х на нее действует сила F упругости растянутой пружины, которая по закону Гука равна:
F = — kx
и направлена к положению равновесия (рис. , б).
При смещении точки влево от О на величину х на нее действует сила F = —kx, направленная вправо, снова к положению равновесия.
Следовательно, при любых смещениях от положения равновесия материальная точка находится под действием упругой силы F = —kx, направленной всегда к положению равновесия О.
Под действием этой силы материальная точка т совершает колебательное движение.
Чтобы материальная точка совершала колебательное движение, не обязательно, чтобы на нее действовали именно упругие силы.
Пример колебательного движения
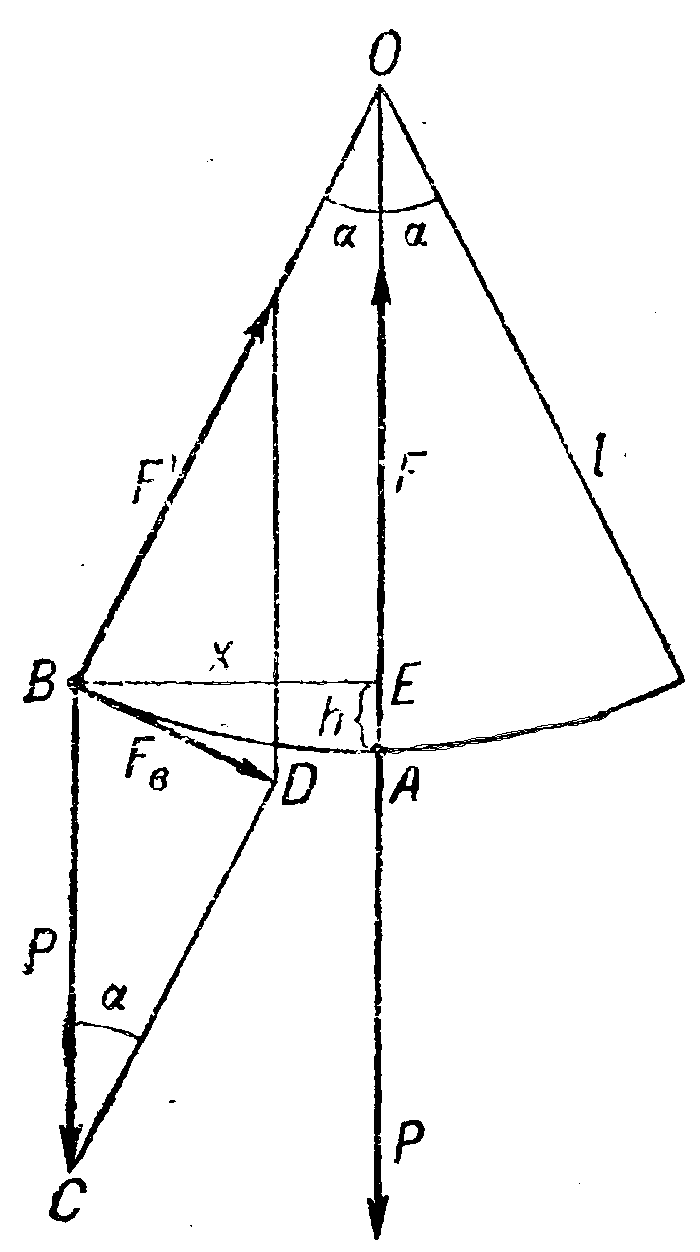
Всю массу шарика будем считать сосредоточенной в центре тяжести его. Если отклонить этот маятник на некоторый угол от положения равновесия и затем отпустить, он придет в колебание.
Достигая положения равновесия, маятник будет каждый раз переходить через него по инерции.
При небольшом угле отклонения (до трех градусов) колебания шарика можно считать прямолинейными.
Пусть маятник (рис. 2) находится в положении равновесия OA. В этом случае равнодействующая силы тяжести Р и силы реакции нити F, приложенных к материальной точке, равна нулю.
Если отклонить маятник на небольшой угол а, то равнодействующая тех же сил уже не будет равна нулю и будет служить возвращающей силой. Очевидно, что эта сила тем больше, чем больше угол а.
Обозначим длину нити буквой l, а за смещение х приближенно примем вместо хорды А В длину перпендикуляра ВЕ, опущенного из точки В на положение равновесия нити OA.
Чтобы найти равнодействующую силу Fb, построим ∆BCD. В нем угол при вершине С равен α, так как его стороны параллельны OA и ОВ. Из подобия ∆BCD и ∆ ВОЕ можно составить пропорцию
FB/P = — (x/l),
или
FB = — (FB/l).
Минус в формуле необходим, так как Fb всегда направлена к положению равновесия, а смещение х отсчитывается от положения равновесия.
Заменив в полученной формуле силу тяжести ее значением, получим формулу для вычисления действующей на маятник возвращающей силы
FB = — ((xmg)/l)
В этой формуле т и l — постоянные величины, g также постоянно для данного места Земли. Поэтому действующая на маятник возвращающая сила пропорциональна смещению маятника х при малых углах а.
Коэффициентом пропорциональности является выражение mg/l. Эта сила по своему характеру аналогична упругой силе.
Силы, неупругие по своей природе, но аналогичные им по виду зависимости от смещения (F = —kx), называются квазиупругими.
Приведенные выше примеры показывают, что действие упругой или квазиупругой силы вызывает колебательное движение.
Периодические колебания
Периодические колебания, совершающиеся под действием силы, пропорциональной смещению и направленной к положению равновесия (под действием упругой или квазиупругой силы), называются гармоническими (простыми) колебаниями.
Если в формулу F = —kx, определяющую гармоническое колебание, подставить, согласно второму закону Ньютона, вместо F произведение та, то получим: та = —kx. Откуда а = — (k/m)х.
Следовательно, при гармонических колебаниях ускорение всегда прямо пропорционально величине смещения и направлено к положению равновесия.
При приближении колеблющейся точки к положению равновесия вектор скорости и вектор силы (ускорения) направлены в одну же сторону параллельно, и скорость возрастает, достигая наибольшего значения в положении равновесия.
При удалении равновесия скорость и сила (ускорение) направлены противоположно, движение происходит замедленно и в крайних точках скорость равна нулю.


Добавить комментарий
Для отправки комментария вам необходимо авторизоваться.