Свободные и вынужденные колебания Резонанс
Колебания, которые совершает тело, выведенное из положения равновесия внешней силой, а затем предоставленное действию внутренних упругих сил, называются свободными колебаниями.
Свободные колебания, происходящие в идеальной системе, в которой нет потерь на трение, называются собственными колебаниями. Частота (или период) собственных колебаний, называемая собственной частотой (или периодом) колебания, обусловлена только свойствами самой системы. Например, период колебания горизонтального пружинного маятника прямо пропорционален корню квадратному из отношения массы т маятника к коэффициенту k упругости пружины:
Т = 2π√(m/k)
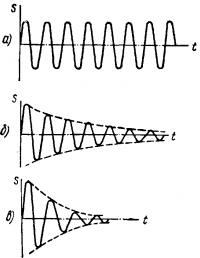
Амплитуда собственных колебаний остается постоянной, в связи с чем колебания называются незатухающими (рис. , а). В реальных условиях амплитуда свободных колебаний постепенно уменьшается. Такие колебания называются затухающими (рис. 2, б и в). Частота колебаний в этом случае несколько отличается от собственной частоты; обычно этим пренебрегают.
Затухание колебаний обусловливается потерей энергии на преодоление сил сопротивления, которое встречает колеблющееся тело в реальных условиях. В основном это различные виды трения (трение между частями самой колеблющейся системы, трение о воздух и т. п.). Чем больше эти потери энергии, тем быстрее затухают колебания.
Убывание амплитуд затухающего колебания происходит таким образом, что каждая последующая амплитуда находится в постоянном соотношении с предыдущей. Закон убывания амплитуд можно показать графически, соединив плавной кривой их крайние точки (пунктир на рис. , бив).
Полученная кривая называется в. математике экспонентой. Убывание амплитуд может быть описано уравнением: at= а0е—δt, где at — амплитуда в момент времени t после начала колебательного процесса, а0—начальная (наибольшая) амплитуда, е — основание натуральных логарифмов, δ — коэффициент
затухания, зависящий от условий, в которых происходит колебание, и характеризующий скорость убывания амплитуд.
Тогда общий вид уравнения для затухающего колебания:
st = а0е—δt sin ωt
Имеются колебательные системы, в которых происходит пополнение энергии, расходуемой колеблющимся телом на преодоление сопротивления, в результате чего колебания имеют незатухающий характер. Например, в часах колебания маятника поддерживаются за счет энергии заведенной пружины, которая, развертываясь, с помощью специального механизма (анкерного спуска) подталкивает маятник при каждом его отклонении.
Такие системы называются автоколебательными, а происходящие в них колебания — автоколебаниями. Частота автоколебаний соответствует собственной частоте колеблющегося тела. Автоколебательная система содержит источник энергии, за счет которой поддерживаются колебания.
Энергия от источника передается колеблющемуся телу в определенные моменты времени с помощью устройства, которое управляется самим колеблющимся телом, и называется устройством обратной связи. Автоколебательной системой является, например, часовой механизм, в нем маятник — колеблющееся тело, заведенная пружина — источник энергии, анкерный спуск — механизм обратной связи.
Что такое вынужденные колебания
Колебания, вызываемые и поддерживаемые действием внешней силы, периодически изменяющейся по величине и по направлению, называются вынужденными колебаниями. Вынужденные колебания — незатухающие, при установившихся колебаниях частота их соответствует частоте изменения внешней силы.
Вынужденные колебания также можно продемонстрировать с помощью пружинного маятника. Для этого рамка Е, в которой закреплены пружины, скрепляются с устройством, приводящим ее в колебательное движение; в данном случае это электродвигатель Д с кривошипным механизмом. При этом со стороны рамки (через пружины) на тело С будет действовать внешняя сила, периодически изменяющаяся по величине и по направлению, которая будет вызывать и поддерживать его колебания.
Если частота изменения внешней силы приближается к собственной частоте колебаний тела, то амплитуда его вынужденных колебаний увеличивается. Причина этого явления в том, что чем ближе эти частоты между собой, тем благоприятнее сочетается действие внешней силы с действием внутренних упругих сил и инерции тела. При полном совпадении этих частот амплитуда вынужденных колебаний резко возрастает. Это явление называется резонансом.
Что такое резонанс
Резонанс это значительное увеличение амплитуды вынужденных колебаний, происходящее при совпадении частоты изменения внешней силы с собственной частотой колеблющегося тела.
Явление резонанса можно наблюдать на пружинном маятнике, если постепенно изменять скорость вращения электродвигателя Д и, следовательно, частоту изменения внешней силы, действующей на тело С. При этом амплитуда колебаний маятника сначала остается почти неизменной, затем постепенно, а при определенной частоте довольно резко возрастает до некоторого максимума и, наконец, сначала также резко, а затем постепенно снижается до исходных значений.
График изменения амплитуды колебаний маятника в зависимости от изменения частоты действующей силы называется кривой резонанса. Максимальная амплитуда колебаний имеет место при частоте, равной собственной частоте маятника. Форма кривой резонанса, ее острота в значительной степени зависят от затухания, свойственного свободным колебаниям данного тела: чем меньше затухание, тем острее резонанс и тем больше возрастает при этом амплитуда колебаний.
Для системы с большим затуханием частота, при которой наступает резонанс, несколько меньше собственной, хотя разница эта невелика.
Явление резонанса имеет место не только при механических колебаниях, но и при колебаниях любой природы, например звуковых, электрических и др. При этом в одних случаях резонанс является положительным явлением, так как позволяет действием незначительной возбуждающей силы вызвать колебания с относительно большой амплитудой. В этом отношении резонанс широко используется в технике приема и усиления звуковых или электрических колебаний.
В других случаях, наоборот, резонанс является вредным явлением, так как может вызвать увеличение амплитуды колебаний выше допустимых (или безопасных) пределов. С этим приходится считаться, например, в машиностроении. Резонанс предупреждают тем, что собственную частоту колеблющейся системы делают значительно отличающейся от частоты действующей силы.
Сложное колебание Гармонический спектр
Колебательное движение, при котором смещение изменяется во времени по любому другому закону, кроме закона синуса или косинуса, называется сложным колебанием. Сложное колебание может быть представлено как результат сложения простых колебаний, что значительно упрощает его анализ.
На основании этих примеров можно установить, что:
а) при сложении двух гармонических колебаний одинакового периода получается гармоническое колебание того же периода;
б) при сложении двух гармонических колебаний различного периода получается сложное колебание. Период этого колебания равняется большему из периодов складываемых колебаний.
Рассмотренный прием сложения простых, одинаково направленных колебаний разного периода, в результате которого было получено сложное колебание, дает основание утверждать о возможности и обратного приема, т е. разложения сложного колебания на простые гармонические.
В общем виде этот вопрос был решен математиком Фурье, который доказал, что любое сложное периодическое колебание может быть представлено суммой простых (гармонических) колебаний, периоды или частоты которых кратны периоду или частоте данного сложного колебания.
Совокупность простых колебаний, на которые можно разложить данное сложное колебание, называется его гармоническим спектром.
В гармоническом спектре колебания указываются частоты и амплитуда всех составляющих eго простых колебаний. Обычно спектр изображается в виде графика, на горизонтальной оси которого откладываются частоты; затем для каждой из частот, имеющихся в спектре простых колебаний, строится ордината, соответствующая амплитуде этого колебания.
Если гармонический спектр сложного колебания содержит только небольшое число простых колебаний и график его состоит из отдельных ординат, то такой спектр называется линейчатым. Если спектр содержит простые колебания практически всех частот, в каких-то пределах, то он называется сплошным и график его строится в виде кривой
Разложение сложного колебания на простые (гармонические) или другими словами нахождение его гармонического спектра является основным приемом при анализе сложного колебания. Часто это делается с помощью специальных приборов, называемых гармоническими анализаторами. Подобные приборы применяются также и в медицине при специальных исследованиях колебательных процессов, например колебаний биопотенциалов мозга и т. п.
Статья на тему Свободные колебания