Поперечные механические волны (примеры формула)

Что такое поперечные механические волны

Если частица вещества, находящаяся в колебательном движении, имеет упругую связь с соседними частицами, то она вовлекает их в колебательное движение, которое таким, образом будет постепенно распространяться в окружающей среде. Явление распространения колебаний в среде называется волновым движением или просто волной. В данном случае это будет упругая механическая волна. К упругим волнам относятся звуковые и ультразвуковые волны, а также волны, образующиеся в земной коре при землетрясении и др.

Пример образования поперечных волн

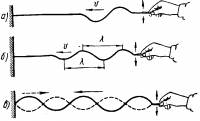
Образование простейшей механической волны можно наблюдать на закрепленном за один конец упругом резиновом шнуре, если второй его конец привести в колебательное движение в направлении, перпендикулярном оси шнура (рис.).

Рассмотрим этот процесс подробнее. Представим себе ряд точек, расположенных на прямой а (рис. 2, а), которые связаны упругими силами так, что смещение одной точки влечет за собой смещение соседних точек. Пусть крайняя точка, совершая гармоническое колебание, в начальный момент времени смещается вниз, увлекая за собой и соседние точки. Через одну четверть периода колебания первая точка будет иметь максимальное смещение.

Соседние точки при этом займут некоторые промежуточные положения (рис. 2, б). Затем крайняя точка начнет возвращаться к среднему положению, однако каждая из соседних точек будет по инерции отклоняться до наибольшего смещения, увлекая при этом за собой последующие точки. Через половину периода колебания первой точки остальные точки займут положение рис. 2, в.

Затем крайняя точка смещается вверх, увлекая за собой и соседние точки, возвращающиеся в среднее положение. В то же время смещение в первоначальном направлении (вниз) будет распространяться на все большее число точек и через три четверти периода колебания крайней точки получится картина, показанная на рис. 2,г. 

Наконец, совершив полное колебание» т. е. через один период, крайняя точка возвратится в среднее положение, а остальные точки займут положение, изображенное на рис. 2, д.

Таким образом колебательный процесс постепенно распространяется от точки к точке среды. Важно отметить, что колебания каждой последующей точки среды происходят все с большим и большим запаздыванием по фазе относительно колебания крайней (начальной) точки.

Если колебания начальной точки поддерживаются, то колебательный процесс захватывает все большее и большее количество точек и волна распространяется все дальше и дальше (рис. б).

Где образуются поперечные волны

Рассмотренная волна является поперечной. Поперечной волной называется волна, распространяющаяся в направлении, перпендикулярном направлению колебания частиц. Поперечные механические волны образуются только в твердых телах, а также на свободной поверхности жидкости, где роль упругой силы играют силы тяжести и поверхностного натяжения, стремящиеся обеспечить горизонтальный уровень свободной поверхности жидкости.

В поперечной волне частицы среды в направлении распространения волны не смещаются. Однако глаз воспринимает движение волны (например, волны на упругом шнуре). Это связано с запаздыванием по фазе колебаний каждой последующей частицы, вследствие чего гребни или впадины волны, более заметные для глаза наблюдателя, перемещаются в направлении распространения волны (см. рис. 3 б).

Волна характеризуется теми же величинами, как и вызывающее ее колебание: периодом Т или частою v амплитудой а, а также формой колебания, обусловливающей и форму волны. По форме волны также разделяются на простые (гармонические) и сложные.

Кроме этого, волна имеет особую, весьма важную характеристику, связанную со скоростью υ распространения колебаний в среде и называемую длиной волны λ. Длина волны это расстояние, на котором смещения точек среды претерпевают изменения, соответствующие одному периоду колебаний. Или проще: длина волны — это расстояние, на которое колебания распространяются в среде за время, равное одному периоду колебания.

Применительно к этому определению длина волны как путь, который волна проходит за время Т одного периода колебания, равняется

λ = υТ = υ/v

где v — скорость распространения волны, v — частота колебания.

Таким образом, длина волны численно равняется произведению периода колебания на скорость распространения волны или отношению скорости распространения волны к частоте колебания.

Скорость распространения волны зависит от свойств среды, поэтому при переходе волны из одной среды в другую длина волны изменяется, хотя частота колебаний остается неизменной.

Длина волны может быть определена так же, как расстояние между двумя ближайшими точками, совершающими колебания в одинаковых фазах.

Составим уравнение простой (гармонической) волны, т. е. формулу, которая позволяет определить в заданный момент времени t смещение s точки Б, расположенной на любом расстоянии х от начальной точки А по направлению распространения волны (рис. 43, а) Для начальной точки уравнение колебания имеет вид:

s_A = a sin ωt = a sin (2πt/T) = a sin 2πvt.

Точка Б начинает колебание с запаздыванием на промежуток времени

t₀. за который волна распространяется от точки А до точки Б:

t₀ = x/υ

где υ — скорость распространения волны в среде.

Применяя уравнение для запаздывающего по фазе колебания, можно написать для точки Б:

s_Б = a sin (ωt — φ₀) = a sin (2π/T)(t —t₀) = a sin 2πv (t — t₀).

Подставляя в формулу значение t₀, получим:

s_Б= a sin (2π/T)(t —x/υ) = a sin 2πv(t —x/υ)

Если вместо скорости волны υ задана длина волны X, то уравнение легко преобразуется:

s_Б= a sin (2π/T)(t/T —x/λ) = a sin 2πv(vt —x/λ)

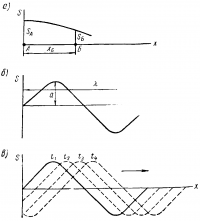
Уравнение волны содержит две переменные величины: время t и расстояние х. При построении графика волны в соответствии с этим уравнением время принимается постоянным (t =const), тогда график дает смещения различных точек среды в зависимости от расстояния х их от начальной точки в некоторый заданный момент времени t. Для простой (гармонической) волны график имеет форму синусоиды (рис. 3, б).

Для других (последующих) моментов времени t₁, t₂, график волны смещается вдоль оси х со скоростью υ распространения волны. Соответствующие кривые показаны на рис. 3, в пунктиром.

Что такое пространственная волна

На примере с упругим шнуром была рассмотрена простейшая линейная волна, т. е. волна, распространяющаяся в одном каком-то направлении. В дальнейшем будут рассмотрены волны, распространяющиеся от источника колебаний в среде по всем направлениям и называемые пространственными волнами. Такими волнами являются, например, звуковые волны.

Волна несет с собой энергию. Энергия упругой механической волны состоит из потенциальной энергии деформации вещества, в котором распространяется волна, и кинетической энергии его колеблющихся частиц. Мгновенное значение энергии волны в каждой точке среды является переменной величиной.

Однако среднее значение ее за период колебаний для данной точки среды постоянно. Эта величина для единицы объема среды, в которой распространяется волна, называется плотностью энергии ε_в волны. Она прямо пропорциональна квадрату амплитуды а² и квадрату частоты v² колебания, а также плотности ρ среды:

ε_в = 2π²ρa²v².

Для некоторого объема V среды среднее значение энергии волны

Е_В = ε_ВV

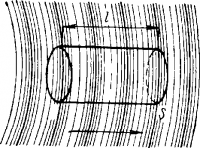
Величина Ps, численно равная средней энергии Е_в, переносимой волной в единицу времени t через заданную поверхность S, перпендикулярную направлению распространения волны (рис. 4), называется потоком энергии через эту поверхность:

Ps = E_в/t

и измеряется в единицах мощности: ватт, эрг в секунду.

Поток энергии, приходящийся на единицу поверхности, перпендикулярной направлению распространения волны, называется плотностью потока энергии:

u = P_s/S = E_в/tS

и измеряется в em/м² и эрг/сек•см². Эту величину называют также интенсивностью волны.

Если источник колебаний имеет достаточную поверхность, то волна распространяется от него равномерным потоком. Такая волна называется плоской. Рассмотрим в этом случае энергию, переносимую частью волны, заключенной в цилиндрическом объеме V среды, расположенном вдоль по направлению движения волны (рис. 44). Промежуток времени t выберем так, чтобы за это время энергия волны, заключенная в объеме V, была бы перенесена через поверхность S, т. е. t = l/υ, где l — высота цилиндра

и υ — скорость распространения волны. Подставляя эти величины в формулу для плотности потока энергии, получим:

u = Е_в/tS = εV/tS = εSl/tS = ε(l/t) = ευ

Плотность потока энергии волны равняется произведению плотности энергии на скорость волны. Отсюда следует, что поток энергии, переносимой волной, можно рассматривать как вектор, совпадающий по направлению с вектором скорости волны. Этот вектор называется вектором Умова.

Если источник колебаний может рассматриваться как точечный, то в однородной среде волна от него распространяется во все стороны равномерно, т. е. имеет сферическую форму. Поверхности сфер относятся как квадраты их радиусов r², также будут относиться и подобные одна другой поверхности S_l, S₂, … на сферах, через которые проходит один и тот же поток энергии P_s. Поэтому плотность потока энергии и по мере удаления от точечного источника колебаний изменяется обратно пропорционально квадрату расстояния:

u₁/u₂ = P_S/S₁ : P_S/S₂ = S₂/S₁ = r²₂/r²₁

Статья на тему Поперечные механические волны