Огюстен Жак Френель

ной лет поступил в Политехническую школу. Оттуда он перешел в Школу мостов и дорог, по окончании которой работал по ремонту и прокладке дорог в Вандее и других округах Франции. Не чувствуя в себе организаторских способностей, Френель тяготился своей работой и пытался отвлечься научными занятиями то в области философии и богословия, то в области техники и химии. Наконец, прочитав сообщение о мемуарах Био, посвященных поляризации, он заинтересовался этим явлением и начал заниматься оптикой.
Но политические события: бегство Наполеона с Эльбы и его победа — привели к отставке роялиста Френеля. С апреля 1815 г. до нового назначения в декабре 1815 г. он напряженно занимался научной работой и 15 октября 1815 г. представил в Академию наук свой первый мемуар по дифракции света. За первым трудом последовал ряд других, стяжавших Френелю мировую славу. В 1823 г. он был избран членом Академии наук. Но уже в 1824 г. болезнь заставила Френеля отойти от научной деятельности. 14 июля 1827 г. он умер.
Рис. О. Френель
В своем первом мемуаре о дифракции света, «в котором специально изучается явление цветных каемок, наблюдающихся у цветных теней, отбрасываемых телами, освещенными светящейся точкой», Френель рассматривает дифракцию от проволоки и отражение и преломление света с точки зрения волновой теории. Он начинает с критики корпускулярной теории света Ньютона. Френель считает сомнительным отсутствие взаимодействия световых частиц среды, в которой свет распространяется. А между тем свет распространяется в воздухе, почти с неизменной скоростью.
Различие в цветах нельзя объяснить различием в скоростях частиц и, следовательно, приходится допустить «такое количество сортов световых частиц, сколько имеется цветов или различных оттенков в солнечном спектре». «Приступы легкого отражения и легкого прохождения почти необъяснимы в системе Ньютона»,— пишет далее Френель. Он указывает, что явление двойного преломления «заставило Ньютона допустить еще одну гипотезу, которая является весьма необычайной, а именно, что световые частицы имеют полюсы…» Вот это обилие гипотез и заставляет Френеля сделать вывод, что «теория колебаний лучше подходит для объяснения всех этих (т. е. световых) явлений, чем теория Ньютона».
Наиболее существенным возражением против волновой теории было прямолинейное распространение света. «Это возражение,— пишет Френель,— единственное, на которое мне кажется затруднительным дать исчерпывающий ответ.
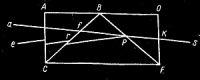
С изумительной изобретательностью и мастерством Френель ставит опыты по дифракции света. Он получает светящуюся яркую точку с помощью «весьма выпуклой линзы», в качестве которой он «использовал шарик меда, помещенный на небольшом отверстии, сделанном в медном листе». «Освещенная этим шариком железная проволока, каемки которой я измерял, давала еще весьма четкие изображения, даже в том случае, когда она находилась на расстоянии только одного сантиметра от световой точки». Френель показал, что дифракционные полосы являются результатом интерференции лучей, идущих от краев проволоки: «каемки образуются в результате перекрещивания этих лучей». Он нарисовал картину волнового интерференционного поля и показал, что «ширины этих каемок, измеренные на различиных расстояниях от проволоки, не являются ординатами прямой линии, но ординатами гиперболы, абсциссами которой являются эти расстояния».
Ньютон в одном из писем, рассматривая некоторые вопросы акустики, изобразил пересекающиеся системы волн, распространяющихся от двух одинаковых источников. Ту же карг тину изображает теперь Френель, но источниками волн у него служат края препятствия. Френель ясно видит стационарное распределение максимумов и минимумов волнового поля, расположенных на гиперболоидах вращения. Ньютон этой картины не увидел, хотя в «Началах» описывает случай погашения волнового движения другим, находящимся в противофазе.
Френель в своих опытах измерил длины волн различных цветов по формуле y =bd/2c где у — ширина полосы, b — расстояние от проволоки до экрана, с — ширина проволоки, d — длина волны. Принцип интерференции дал возможность Френелю объяснить законы отражения и преломления тем, что световые колебания погашают друг друга для всех направлений, кроме направлений, удовлетворяющих закону отражения или закону Снеллиуса—Декарта. Из своей теории Френель сделал вывод, противоположный выводу Ньютона, а именно, «что скорость света в стекле меньше, чем скорость света в воздухе».
Опыты с кольцами Ньютона Френель воспроизвести не мог, не имея соответствующих линз. Однако в дополнениях ко второму мемуару, представленных в Академию наук 15 июля 1816 г., Френель уже описывает опыт с кольцами Ньютона и интерпретирует его в духе волновой теории. Здесь же он дает теорию интерференции в плоскопараллельных пластинках и выводит формулу для разности хода интерферирующих лучей, приводимую теперь во всех курсах физики (d—2xcosi, где х — толщина пластинки, i— угол преломления).
Наконец, в этом же дополнении он описывает свой классический опыт с зеркалами. Френель отмечает, что этот опыт удался ему лишь «после нескольких неудачных опытов». «Мимоходом отмечу,— пишет он,— что лишь теория колебаний могла привести к идее постановки такого рода опыта. Этот опыт настолько труден, что почти невозможно, чтобы чистый случай на него натолкнул».
В самом втором мемуаре, опубликованном в мартовском номере «Анналов химии и физики», Френель воскрешает забытый принцип Гюйгенса: «Наиболее естественная гипотеза состоит в том, что молекулы тела, приведенные в колебание падающим светом, становятся центрами испускания новых волн». Дополняя принцип Гюйгенса принципом интерференции, Френель превращает геометрический принцип в физический и успешно решает с его помощью ряд дифракционных задач.
Принцип интерференции, который Френель довольно неясно формулирует в своем первом мемуаре, был, как мы видели, уже сформулирован Юнгом, и Араго сказал об этом Френелю. Френель в своем письме к Араго от 23 сентября 1815 г. пишет, что он, не зная английского языка, не мог прочитать этой книги. Через месяц Френель сообщает Араго: «Очень простой эксперимент доказал мне, что световые лучи могут действовать друг на друга, ослабляться и даже почти совершенно погашаться, когда колебания мешают друг другу, и, наоборот, добавляться и взаимно усиливаться, когда они колеблются. На этом принципе я основываю свое объяснение дифракции». Френель совершенно независимо от Юнга пришел к принципу интерференции. Только от Араго он узнал о том, что то же самое открыл Юнг.
Франсуа Доминик Араго (1786— 1853) сыграл большую роль в развитии и пропаганде волновой теории. Он содействовал приезду
Френеля в Париж в 1816 г., где в течение десяти месяцев Френель выполнял ряд опытов по дифракции и интерференции. В начале 1817 г. Парижская Академия предложила на премию задачу о дифракции, формулируя ее следующим образом;
«1) Определить с помощью точных опытов все эффекты дифракции световых лучей прямых и отраженных, когда они проходят одновременно или раздельно вблизи границ одного или нескольких тел, ограниченных или бесконечных, принимая во внимание расстояния между этими телами, равно как и расстояние до источника света, откуда исходят лучи.
2) С помощью математической индукции вывести из этих опытов движения лучей при их прохождении вблизи тел».
Сама формулировка задачи не оставляет сомнения, что авторы ее явно имели в виду корпускулярную теорию света. Их интересовала теория движений световых частиц вблизи самих дифрагирующих тел. Во взаимодействии
световых корпускул с молекулами тел они усматривали «секрет физического процесса, благодаря которому лучи изгибаются и разделяются на различные полосы разного направления и интенсивности». Френель колебался, принять ли участие в конкурсе, но уговор друзей и поддержка младшего брата Фюльжане, помогавшего ему в опытах, возымели свое действие, 20 апреля 1818 г. он представил в Академию в запечатанном конверте «Записку о теории дифракции».
В первых же параграфах этой записки он показывает, что эмиссионная теория света не в состоянии объяснить явление дифракции. Молекулярные взаимодействия не распространяются на такие значительные расстояния, которые достигают полмиллиметра. Массы краев дифрагирующего тела не играют никакой роли: «Нить и обушки бритвы дают совершенно одинаковые явления». Френель описывает опыт с дифракцией света, проходящего между двумя близкими стальными пластинками, вертикальные края которых с одной стороны были острыми, а с другой — округленными. Он помещал острый край против закругления и наоборот и не заметил никакого изменения дифракционной картины: полосы были прямыми, как будто бы обе пластинки были обращены друг к другу одинаковыми краями. Из этого опыта следует, что явления дифракции совершенно необъяснимы с точки зрения эмиссионной теории. «Волновая теория, как мне кажется, наоборот, приводит к полному объяснению этих явлений при помощи принципа Гюйгенса, который можно сформулировать следующим образом: колебания световой волны в каждой из ее точек равны сумме всех элементарных движений, которые были бы посланы в один и тот же момент каждой действующей изолированной частью этой волны, рассматриваемой в каком-нибудь одном из своих предыдущих положений».
Применяя свой расчет к случаю дифракции от края экрана, он находит «периодические изменения интенсивности света по мере того, как свет удаляется от края геометрической тени».
Комиссия в составе Био, Араго, Лапласа, Гей-Люссака и Пуассона присудила премию мемуару под девизом «Natura simplex et fecuna» (Природа проста и плодотворна), т. е. Френелю, написавшему этот девиз на конверте. При обсуждении работы возник следующий эпизод, описанный в докладе комиссии и прочитанный Араго: «Один из членов нашей комиссии — г-н Пуассон — вывел из сообщенных автором интегралов тот удивительный результат, что центр тени от круглого непрозрачного экрана должен быть таким же освещенным, как и в том случае, если бы экран не существовал,— это при условии, что лучи проникают в тень под малыми углами падения. Это заключение было проверено прямыми опытами, и наблюдение полностью подтвердило данные вычисления». Расчеты Пуассона Араго проверил на опыте, превратив таким образом возражение Пуассона в убедительнейшее доказательство справедливости теории Френеля.
Следует отметить, что свет в центре тени круглого экрана (шарика) наблюдал еще в 1715 г. Ж. Н. Делиль (1688—1768), бывший с 1726 по 1747 г. членом Петербургской Академии наук.
Премированный мемуар Френеля о дифракции был в своей значительной части опубликован в двух статьях в «Анналах физики и химии» за 1819 г. Полностью он был напечатан в «Трудах Парижской Академии» за 1826 г.
Мемуар открывается рассмотрением двух систем, «которые до сего времени разделяли ученых в их воззрениях на природу света». Здесь интересен философский аргумент в пользу волновой теории, выраженный латинским эпиграфом «Природа проста и плодотворна» и принципом: природа создает максимум явлений при помощи минимума причин. Френель указывает, что хотя и «очень трудно открыть основания этой замечательной экономии», но этот «общий принцип философии физических наук… может направлять усилия человеческого ума».
Конкретный материал мемуара Френеля очень богат. Он описывает опыты и измерения различных случаев дифракции и интерференции. При этом он постоянно обращает внимание на неудовлетворительность эмиссионной теории, на ее неспособность объяснить описываемые явления без противоречий и сомнительных допущений. Он показывает, что волновая теория легко объясняет эти явления путем суперпозиции волн, и выводит основную формулу интерференции:
A2 = a2 + a‘2 + 2aa’ cos(2π(c/λ))
которая сегодня вошла во все учебники физики. Помимо интерференционного опыта с зеркалами, Френель описывает опыт с бипризмой. В этом же мемуаре он дает новую формулировку принципа Гюйгенса и развивает метод зон, ныне также вошедший во все учебники. Мемуар заполнен таблицами расчетов различных случаев дифракции. Особо автор разбирает дифракцию от круглого экрана и круглого отверстия, используя свой метод зон. Мемуар заканчивается объяснением преломления света по волновой теории.
Теперь оставалось подчинить волновой теории явления поляризации и хроматической поляризации. Изучая интерференцию поляризованных лучей, Френель еще в 1816 г. отмечал, что волновая теория «пока что не дала объяснения явлению поляризации», и добавлял, что, по-видимому, для такого объяснения она должна быть видоизменена; «эта модификация света состоит в поперечности световых волн». Однако предположение о поперечности световых волн, как отмечал Френель, «настолько противоречило принятым представлениям о природе колебания упругих жидкостей, что прошло немало времени, прежде чем я принял его окончательно».
Юнг, «более смелый в своих предположениях», сообщил эту идею в письме к Араго от 12 января 1817 г. Но Френель, который пришел к идее поперечности световых волн раньше Юнга, не торопился публиковать ее. Он хорошо понимал, в какое противоречие вступает эта гипотеза с механикой упругих сред. Только тщательные эксперименты и прежде всего установленный им и Араго факт, что лучи, первоначально поляризованные во взаимно перпендикулярных плоскостях, не интерферируют, даже если их привести к одной плоскости поляризации, заставили его принять гипотезу поперечности световых волн.
Френель, высказав идею, что поперечные колебания в линейно поляризованном свете совершаются в одной плоскости, перпендикулярной плоскости поляризации, определил обычный свет «как совокупность, или, точнее, как быструю последовательность систем, поляризованных по различным направлениям волн». Акт поляризации, по Френелю, «состоит не в создании этих поперечных движений, а в разложении их по двум перпендикулярным неизменным направлениям и в отделении составляющих друг от друга».
Рис. Параллелепипед Френеля
В этой смелой гипотезе, настолько смелой, что даже ревностный сторонник Френеля Араго отступил, не отважившись следовать за ним, мы видим один из ярких примеров того, как наука идет от «явного для нас» к «явному по природе», вопреки сложившимся представлениям и традициям. Френель задал на многие годы головоломную задачу теоретикам, каким образом эфир, настолько тонкий, что не оказывает никакого сопротивления движению сквозь него небесных тел, вместе с тем не оказывает упругого сопротивления сжатию и расширению, а упруго сопротивляется только деформациям сдвига. Это свойство роднит его с твердым телом, а не с жидкостью или газом, притом таким твердым телом, которое абсолютно несжимаемо и не допускает продольных волн. Однако гипотеза поперечных волн позволила Френелю построить теорию отражения и преломления света, а также теорию двойного преломления.
В мемуаре «О расчете цветов, которые вызывает поляризация в кристаллических пластинках», опубликованном в «Анналах физики и химии» за 1821 г., Френель излагает основы своей теории поляризации. Он рисует картину поперечных колебаний частиц упругой среды, Очевидно— пишет Френель,— что к этим новым колебаниям, перпендикулярным лучам, можно применять те же рассуждения и вычисления, которые применяются в случае, когда колебательное движение происходит вдоль направления распространения». Это дает ему возможность применить к поляризованному свету принцип интерференции и таким путем объяснить многие оптические явления».
В частности, Френель строит теорию поляризации света при отражении, считая, что при переходе света из одной прозрачной среды в другую упругость эфира не меняется, а меняется его плотность. Вначале он рассчитывает интенсивность отраженного света, поляризованного в плоскости падения, но в добавлении к статье рассматривает и случай отражения света, поляризованного перпендикулярно плоскости падения.
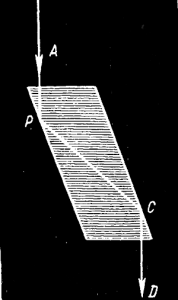
В мемуаре о двойном преломлении, представленном в Академию наук 9 декабря 1822 г., Френель описывает новый поляризационный прибор — стеклянный параллелепипед, известный ныне под названием «параллелепипед Френеля». В этом приборе предварительно поляризованный свет «последовательно, на двух противоположных сторонах, претерпевает два полных внутренних отражения при (предельном) угле падения приблизительно в 50° в плоскости, наклоненной на 45° к первоначальной плоскости поляризации». При этом выходящий из стеклянного параллелепипеда свет «является как будто полностью деполяризованным». Френель выясняет, что на самом деле этот свет «можно рассматривать как состоящий из двух пучков, следующих по одному и тому же пути, но поляризованных в перпендикулярных направлениях и отличающихся в своем ходе на четверть длины волны». Такой свет Френель называет поляризованным по кругу, а самую поляризацию — круговой (циркулярной) поляризацией. «Между прямолинейной и круговой поляризацией существует множество промежуточных поляризаций, которые обладают характерными свойствами обеих поляризаций и которым, исходя из тех же теоретических соображений, можно было бы дать наименование эллиптических поляризаций».
Таким образом, Френель на языке волновой теории полностью описал явление поляризации, и введенные им понятия сохраняют свое значение и сейчас. Он указал методы экспериментального анализа поляризации света, используемые и поныне. К своим опытам он прибавил изящный метод разделения лучей, поляризованных по кругу, в противоположные стороны. Воспользовавшись наблюдением Био, что существуют две модификации кварца (горного хрусталя, по тогдашней терминологии), из которых одна вращает плоскость поляризации вправо, а другая влево, он составил призму из трех частей: входной и выходной одного сорта, промежуточной — другого. Предполагая, что скорости распространения света, поляризованного по кругу влево и вправо, в различных сортах кварца различны, он нашел, что линейно поляризованный свет в такой составной призме разделится на два поляризованных по кругу луча. Они выйдут из выходной призмы, отклонившись в противоположные стороны. «Мы получаем этим способом весьма заметное разделение двух изображений, которое можно было бы еще увеличить, умножая число призм»,— пишет Френель.
7 января 1823 г. Френель представил Академии наук «Мемуар о законе модификаций, которые сообщаются отражением поляризованному свету». Здесь он дает механическое обоснование формул отражения света, поляризованного в плоскости падения, и света, поляризованного в плоскости, перпендикулярной плоскости падения. Если положить, что свет поляризован в плоскости, составляющей с плоскостью падения угол α, и амплитуда колебаний равна 1, то амплитуда составляющей в плоскости падения будет sin α, а составляющей в плоскости, перпендикулярной плоскости падения, будет cos α.
Амплитуды соответствующих составляющих отраженного света будут:
где i — угол падения, i’ —угол преломления Углы падения и преломления связаны, по Френелю, соотношением d — плотность первой среды, d’ — плотность второй среды, упругость же эфира в обеих средах Френель принимает одинаковой.
Из своих формул Френель выводит закон Малюса—Брюстера. Он обосновывает свои формулы законом сохранения живых сил и гипотезой, что движения, параллельные границе раздела, в обеих волнах одинаковы. Из формул Френеля вытекает поворот плоскости поляризации в отраженной и преломленной волнах. Весьма замечательно, что Френель распространил свои формулы и на случай полного отражения, смело введя мнимые величины: для углов, больших предельного, sin i’ становится больше 1, a cos i‘ — мнимым. Френель исходит при этом из того, что формулы, справедливые до предельного угла, должны «в силу общего закона непрерывности» быть правильными и при переходе через этот предел, однако «затруднение заключается в том, как их интерпретировать и как разгадать то, что возвещает анализ в этих мнимых выражениях». Френель разгадал, что же означает мнимое выражение: оно означает изменение фазы в отраженной волне. Обе компоненты испытывают скачки разной величины.
Поразительно, как много сделал Френель за столь короткое время. Им по существу была полностью создана классическая волновая оптика. К описанным выше результатам следует добавить его теорию распространения света в одноосных и двухосных кристаллах, развитую в работах о двойном лучепреломлении в 1821-1822 гг. Френель развил идеи Гюйгенса о распространении волн в одноосных кристаллах. Идеи Гюйгенса он настолько высоко ценил, то ставил их выше всех открытий в оптике Ньютона, утверждая, что открытие Гюйгенса, «быть может, труднее сделать, нежели все открытия Ньютона в области явлений света». Несомненно, что в этом утверждении отразился характер борьбы с эмиссионной теорией, которую вел Френель во всех своих оптических работах.
Для описания распространения света в кристаллах Френель ввел замечательное построение: эллипсоид упругости Френеля. Он установил, что в анизотропной кристаллической среде всегда существуют три прямоугольные оси упругости. Он строит эллипсоид упругости, который дает закон величин упругости анизотропной среды и величину скоростей для различных направлений распространения волн. Этот эллипсоид имеет две диаметральные плоскости, пересекающие его по кругам. Для волн, плоскости которых параллельны этим кругам, всегда имеется одна скорость распространения, каково бы ни было направление их колебаний. Эти направления Френель назвал оптическими осями и показал, что никогда не бывает более двух оптических осей в анизотропных средах. Для одноосных кристаллов поверхность упругости становится поверхностью вращения.
Френель заложил, таким образом, основы кристаллооптики. О том, насколько плодотворным оказался предложенный им метод, можно судить по тому, что в 1832 г. Гамильтон вывел из его теории следствие о существовании в двухосных кристаллах тонкого явления — конической рефракции. Если в таких кристаллах пучок света идет по направлению оптической оси, то он выходит из кристаллической пластинки в виде полого светового конуса (внешняя коническая рефракция). Конический пучок внутри кристалла выходит параллельным цилиндрическим пучком. Это явление невозможно обнаружить эмпирически без помощи теории. Ллойд открыл его в том же 1832 г. экспериментально, руководствуясь теорией Френеля—Гамильтона. Это открытие было блестящим триумфом волновой теории света.
В истории физики важную роль сыграло опубликованное в 1818 г. в «Анналах химии и физики» письмо Френеля Араго по вопросу о влиянии движения Земли на оптические явления. Араго пытался обнаружить это влияние, измеряя разность зенитных расстояний звезды, наблюдаемой непосредственно и через призму. Араго такого влияния не обнаружил. Это дало повод Френелю обсудить на основании волновой теории вопрос о влиянии движения Земли на распространение света в преломляющей среде Френель знает, что «скорость, с которой распространяется волна, не зависит от движения тела, которое ее испускает». Он полагает, что результат Араго можно объяснить, если предположить, «что эфир свободно проходит через земной шар и что скорость, сообщенная этой тонкой жидкости, представляет собой только небольшую часть скорости Земли и не превышает, например, одной сотой доли этой скорости».
Эта гипотеза частичного увлечения эфира помогла Френелю объяснить, почему «видимая рефракция не изменяется с изменением направления световых лучей по отношению к движению Земли», как это обнаружил Араго и позднее Эйри (1871 г.). При этом Френель полагает, что квадраты длин волн в эфире и преломляющей среде относятся как плотности этих двух сред:
d2:d’2 = ∆’: ∆.
Отсюда коэффициент увлечения
где μ — показатель преломления среды.
Френель показывает, что аберрационный эффект не изменится, если трубу телескопа заполнить водой, что и было подтверждено опытом Эйри в 1871 г. Идея этого опыта принадлежала Ружеру Бошковичу. Формула же коэффициента увлечения была подтверждена в 1851 г. опытом Физо, повторенным в 1886 г. Майкельсоном, производившим этот опыт с Морли, и в 1914 г. Зееманом.
Таковы важнейшие результаты, полученные Френелем в оптике. Следует добавить, что Френель не ограничивался теоретическими исследованиями, он стремился сочетать их с экспериментом. Так, всемирную известность приобрела изобретенная им система освещения маяков, в которой важнейшей составной частью была сконструированная им ступенчатая линза, описанная в мемуаре, представленном в Академию наук 29 июля 1822 г.
Статья на тему Огюстен Жак Френель

Добавить комментарий
Для отправки комментария вам необходимо авторизоваться.