Дифракция (волн, света)

Дифракция это отклонение волны или света от прямолинейного распространения, к примеру некоторое огибание волн препятствий на поверхности воды, дифракция света почти не существует но ее можно наблюдать с помощью некоторых приборов или равномерно запыленной пластинки. Дифракцию света можно также наблюдать в полнолуние когда на небе есть как бы туман или зимой в сильный мороз, образуется одинарный или больше кругов во круг луны.

Что такое дифракция волн

Это — любое отклонение волны от прямолинейного распространения. Весьма важным случаем дифракции является огибание волной краев препятствия, расположенного на пути распространения волны.

Рассмотрим дифракцию волн на поверхности воды. Если на пути волны находится достаточно широкое плоское препятствие, например экран Э, то позади него образуется свободное от колебаний пространство, называемое тенью. Края тени ограничены лучами, проведенными из источника у краев препятствия. Если постепенно уменьшать ширину экрана, то волна начинает огибать его края и заходит в область тени на некоторый угол а.

Чем уже будет препятствие, тем сильнее будет огибание его краев волной. Наконец, если ширина препятствия станет близкой к длине волны, то тень исчезнет и волны, огибая препятствие, будут полностью замыкаться на небольшом расстоянии от него (заметим, что применительно к световой волне отсутствие тени означает невидимость тела).

Аналогичная картина получится, если взять широкий экран с отверстием или щелью. При щели, достаточно широкой по сравнению с длиной волны, часть волны, проходящая через нее, сохраняет прямое направление. Постепенно сужая щель, можно видеть, как волна огибает края экрана и заходит за границы щели, причем тем в большей степени» чем уже делается щель. Наконец, когда щель сделается соизмеримой с длиной волны, за ней будет распространяться круговая волна, хотя и значительно более слабая, чем основная волна.

Угол α, на который отклоняются от первоначального направления лучи дифрагировавшей волны называется углом дифракции. Угол дифракции а тем больше, чем меньше ширина препятствия или отверстия, через которое проходит волна, сравнительно с длиной волны. Следовательно, при данной ширине d препятствия или отверстия угол дифракции α тем больше, чем больше длина волны λ, или при данной длине волны λ угол дифракции а тем больше, чем меньше ширина d отверстия или препятствия.

Дифракция волн хорошо объясняется с точки зрения принципа Гюйгенса— Френеля. Возьмем пример дифракции волны при прохождении через узкую щель, перпендикулярную плоскости рисунка. Рассматривая точки поверхности волны, построенной внутри щели, как центры образования вторичных круговых волн, можно построить новую поверхность волны как огибающую к ним.

Выполняя последовательно построение ряда новых поверхностей волны, можно установить, что волна за щелью постепенно расширяется за счет распространения в стороны колебаний от крайних круговых волн. Относительное значение этих волн тем больше, чем меньше ширина щели. Поэтому и дифракция проявляется тем сильнее, чем меньше ширина щели по сравнению с длиной волны. При ширине щели, соизмеримой с длиной волны, можно считать, что в ней возбуждается только одна элементарная круговая волна, которая и распространяется за щелью.

Рассеяние волны

Если в среде, в которой распространяется волна, имеются мелкие инородные частицы или неоднородности в строении самой среды, то волна, достигая их, вызывает образование вокруг них элементарных круговых волн, распространяющихся во все стороны. Интенсивность основной волны при этом ослабляется. Это явление называется рассеянием волны и также относится к дифракции.

Образование рассеянных волн можно показать, если поместить в нашей ванне препятствие, меньшее по размерам длины волны, и затем вызвать ряд отдельных волн. Каждая из этих волн, достигая препятствия, будет вызывать образование вокруг него как центра новой круговой волны, хотя и весьма слабой по интенсивности.

Дифракция света

В практической жизни дифракция света почти не наблюдается. Это связано с тем, что большая часть окружающих тел имеет размеры, значительно превышающие длину волны света. В этом случае дифракцию можно наблюдать только при условии, что световая волна, претерпевшая дифракцию, отбрасывается на достаточно далеко (десятки метров) расположенный экран.

Дифракцию света можно наблюдать с помощью равномерно запыленной стеклянной пластинки (чистую стеклянную пластинку надо слегка протереть маслом, а затем обсыпать, например, ликоподием). Если через пластинку посмотреть на нить горящей электролампы, находящейся на расстоянии 2—3 м,то увидим нить, окруженную цветными кольцами, напоминающими интерференционные полосы.

Эти кольца образуются в результате интерференции лучей, дифрагировавших при прохождении через запыленный слой пластинки. Подобные круги видны в морозный день вокруг солнца; роль пылинок здесь выполняют находящиеся в воздухе мельчайшие кристаллы льда. Цветные круги вокруг светящихся предметов появляются при заболеваниях глаз, связанных с помутнением прозрачных сред самого глаза, и т. д.

Более полную дифракционную картину можно получить, если, например, осветить узкую щель в экране Д достаточно сильным пучком параллельных монохроматических лучей, перпендикулярных плоскости щели, и наблюдать изображение щели на достаточно далеко расположенном экране. Изображение состоит из центральной светлой полосы и по обеим сторонам от нее узких чередующихся темных и значительно менее ярких светлых полос. При освещении щели белым светом получается изображение, состоящее из центральной белой полосы и цветных полос по сторонам.

Дифракционное изображение

Образование дифракционного изображения щели можно объяснить на основании принципа Гюйгенса — Френеля. Отдельные точки поверхности волны, проходящей через щель, могут рассматриваться как центры вторичных круговых волн (рис. 2). Эти волны, распространяясь за пределами щели, интерферируют между собой, и картина, получающаяся на экране Э, зависит от разности хода, образующейся между ними для различных точек экрана.

Дифракционное изображение малого отверстия, освещенного параллельным пучком монохроматических лучей, представляет светлое пятно, окруженное чередующимися темными и светлыми кольцами; при освещении белым светом получается белое пятно, окаймленное цветными кольцами. Наличие интерференционных колец в изображении малого отверстия затрудняет суждение о его форме и величине, а при наличии нескольких близко расположенных отверстий может препятствовать их различению или, как называют в оптике, их разрешению. 

Если изображения видны по отдельности, то тонки разрешены. Если изображения сливаются, включая и центральные пятна, то точки не разрешены. Пределом разрешения по Рэлею является наложение края центрального светлого пятна одного изображения на первое темное кольцо другого .

Дифракционная решетка

Дифракционный спектроскоп. При изучении дифракционных явлений применяется дифракционная решетка. Она состоит из непрозрачной для света пластинки, в которой имеется большое число узких параллельных щелей. Решетка освещается от сильного источника пучком параллельных лучей (дифракция Фраунгофера). Результат дифракции наблюдается на экране, помещенном в фокальной плоскости собирающей линзы, расположенной впереди решетки. Линза фокусирует параллельные лучи, отклонившиеся в результате дифракции в отдельных щелях решетки.

Дифракционная решетка изготовляется из стеклянной пластинки, на которой алмазным острием наносится необходимое количество параллельных штрихов. Штрихи затираются черной краской. Неповрежденное стекло между штрихами служит щелями решетки. Расстояние d между центрами соседних щелей называется периодом или постоянной решетки.

Лучи, дифрагировавшие под различными углами, будут иметь различную разность хода. В зависимости от соотношения разности хода ∆ с длиной волны λ определится результат интерференции: усиление колебаний в точках, для которых разность хода равняется нулю или четному числу полуволн: 

∆_ус = 0; λ

(рис. 3, в); 2λ, 3λ и т. д. или ослабление колебаний при разности хода, равной нечетному числу полуволн:

Д_осл = λ/2

(рис. 3, б); (3/2)λ; (5/2)λ и т. д. В результате дифракционная картина в фокальной плоскости линзы будет состоять из центральной светлой полосы и чередующихся темных и светлых боковых полос, постепенно убывающих по яркости.

Если на дифракционную решетку падает перпендикулярно волна монохроматического света, то между лучами, отклонившимися в каждой щели под углом а, образуется разность хода, кратная разности хода А между двумя соседними лучами: ∆; 2∆; 3∆ и т. д.. В общем случае n∆. Очевидно, что наличие множителя п не нарушает основного соотношения между разностью хода ∆ и длиной волны λ, обусловливающего усиление или ослабление колебаний при интерференции. Поэтому все лучи, имеющие разность хода ∆_ус, равную четному числу полуволн, будут, интерферируя между собой, давать усиление колебаний, а все лучи, имеющие разность хода ∆_осл, равную нечетному числу полуволн, — ослабление колебаний.

Дифракционная картина, наблюдаемая на экране, помещенном в фокальной плоскости линзы, будет подобна случаю двух щелей, но значительно более яркой. Светлые полосы в этой картине называются дифракционными максимумами (темные полосы — дифракционными минимумами) и в зависимости от расположения их по отношению к центральной полосе, называемой нулевым максимумом, различаются по порядку: 1-й, 2-й и т. д.

Относительная яркость дифракционных максимумов показана в виде графика в правой части рисунка. С возрастанием порядкового номера яркость максимумов значительно убывает. Ширина дифракционных максимумов, а также расстояние между ними зависят от периода решетки: чем меньше период, тем шире полосы и тем дальше расположены они от средней линии.

В соответствии с порядком того или иного максимума, обозначаемого буквой m, будет различаться как разность хода ∆, так и угол отклонения α лучей, образующих этот максимум.

Например: для максимума 1-го порядка (m =1): ∆₁ = d sin α₁= λ; для максимума 2-го порядка (m = 2):

∆₂ = d sin α₂ = 2λ

и т. д.; для максимума т порядка:

∆_m = d sin α_m = т λ.

Рассмотрим дифракцию плоской монохроматической волны, падающей перпендикулярно на две узкие параллельные щели (рис. 3). Предположим, что в каждой щели образуется по одной вторичной волне. Эти волны когерентны и за щелями будут интерферировать между собой. Результат интерференции двух параллельных лучей OA и О’А’ (рис. 3, а), которые отклонились в щелях под одинаковым углом а к первоначальному направлению и которые линзой собираются в одну точку фокальной плоскости, зависит от разности хода А, образовавшейся между ними в связи с изменением их направления (преломление лучей в линзе на разность хода не влияет). Если из точки О‘, в которой луч О’А’ изменяет направление, опустить перпендикуляр на луч OA, то О’В есть фронт дифрагировавшей волны, а отрезок ОВ есть разность хода между этими лучами:

∆ = О‘В.

Разность хода А можно выразить через расстояние d между центрами щелей и угол α отклонения лучей: из треугольника ОО’В, в котором угол при вершине О равен углу а, находим:

∆ = d sin α

Последнее соотношение называется формулой дифракционной решетки.

Если на решетку падает белый свет, то положение максимумов одного и того же порядка для лучей с различной длиной волны будет разным, в результате чего каждый максимум состоит из системы цветных полос, которая называется дифракционным спектром.

Максимумы нулевого порядка, совпадая для всех длин волн, дают центральную белую полосу О, максимумы первого порядка отделены от нее темными промежутками N и образуют отчетливые картины спектров первого порядка, фиолетовые полосы которых расположены ближе к центру, а красные — дальше от центра. Дальше располагаются спектры более высоких порядков, однако в них уже может происходить наложение цветных полос спектров различного порядка.

В связи с тем что расположение цветных полос в дифракционном спектре более равномерно, чем в спектре, который получается с помощью призмы, этот спектр называется нормальным спектром.

Дифракционный спектроскоп

С помощью дифракционной решетки может быть измерена длина волны светового излучения. Прибор называется дифракционным спектроскопом и устроен аналогично призменному спектроскопу, только вместо призмы в центре диска Д устанавливается дифракционная решетка. При измерении зрительная труба з устанавливается по направлению соответствующего максимума. Угол α_т, измеренный при этом по шкале диска Д, равен углу, под которым отклоняются лучи, образующие этот максимум. Длина волны λ находится по формуле дифракционной решетки: λ = d sin α_m, где d— период решетки.

Длины волн, соответствующие основным цветам спектра, приведены в таблице.

Цвет	Длина волны в ммк
Красный	760—620
Оранжевый	620—590
Желтый	590—575
Желто-зеленый	575—550
Зеленый	550—510
Голубой	510—480
Фиолетовый	450—380

Дифракция при наклонном падении лучей на решетку

Рассмотрим дифракцию пучка параллельных монохроматических лучей, падающих на решетку под углом φ: проходя через щели, лучи вследствие дифракции отклоняются от первоначального направления в обе стороны на некоторые углы γ’ и γ«. Эти углы определяют направления на соответствующие дифракционные максимумы. Обозначим α₁‘ и α₂» углы, образуемые этими лучами, с перпендикуляром к плоскости решетки, который является оптической осью системы.

Для наших рассуждений существенно то, что при одной и той же степени дифракции угол α’ отклонения от оптической оси системы для лучей OA’ при любом угле падения φ будет меньше, а угол α» для лучей OA» больше, чем соответствующие углы при перпендикулярном падении лучей на решетку.

Поскольку лучи OA’ с меньшим отклонением от оптической оси системы будут использованы в дальнейшем изложении, определим для них разность хода при образовании максимумов того или иного порядка. При этом углы отклонения лучей будем отсчитывать от оптической оси системы. Для этого из точки изменения направления хода первого луча опустим перпендикуляры bа и bd на второй луч.

Отрезки ас и cd в сумме образуют расстояние, на которое путь второго луча больше, чем путь первого. Разность хода лучей ∆₁‘ = ac + cd. Из треугольников abc и cbd отрезки ас и cd можно выразить через период d решетки и углы при вершинах этих треугольников, равные углам падения и отклонения дифрагированных лучей:

ас = d sin φ иcd = d sin α’₁.

Следовательно,

∆₁‘ = ас + cd — d sin φ + d sin α’₁ = d (sin α’₁ + sin φ).

Максимум нулевого порядка будет располагаться по направлению падения лучей (разность хода ∆₀ =0), максимум первого порядка — по угловому направлению, обусловленному соотношением

∆₁‘ = d (sin α’₁ + sin φ) = λ и т. д.

Лучи OA» представляют для нас меньший интерес. Заметим только, что, ориентируясь на систему этих лучей, можно получить большое отклонение лучей от оптической оси системы даже при малой степени дифракции, т. е. на грубых решетках с большим периодом, дифракция на которых при перпендикулярном падении лучей почти незаметна.

Рассеяние света

Одним из видов дифракции является рассеяние света на неоднородностях среды, через которую свет проходит. Прямой свет, падая на мельчайшие неоднородности среды, изменяет направление таким образом, что распространяется от них во все стороны, в связи с чем. они наблюдаются как слабо светящиеся точки (несамостоятельное свечение).

Рассеяние света может происходить, например, на частицах пыли или дыма в воздухе, на частицах тумана, на мелкодисперсной эмульсии жира в воде и т. д. Подобные среды называются мутными, а рассеяние света на них — эффектом Тиндаля.

Рассеяние света в мутной среде

Рассеяние света в мутной среде можно продемонстрировать следующим опытом. В энергично перемешиваемую воду вливают несколько капель спиртового раствора канифоли; спирт смешивается с водой и канифоль выделяется в виде мельчайших, не различимых глазом твердых частичек. Если через такую среду пропустить узкий пучок света, то он будет виден сбоку в виде слабо светящейся полоски, прямые лучи при этом сильно ослабляются (рис. 4, а). Аналогичное явление можно наблюдать, когда узкий пучок лучей проходит сквозь запыленную атмосферу: свет рассеивается на пылинках и весь пучок становится видимым в любом направлении.

Рассеяние света на пространственных неоднородностях среды происходит тем интенсивнее, чем мельче эти неоднородности сравнительно с длиной волны света.

С точки зрения принципа Гюйгенса в основе рассеяния света лежит образование вторичных круговых волн, возбуждаемых первичной волной падающего света, вокруг центров, которыми являются мельчайшие неоднородности среды. Эти волны и являются волнами рассеянного света.

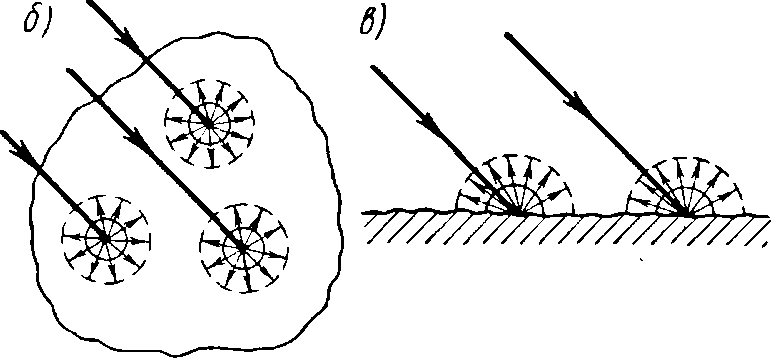
Если рассматривать ход лучей, то явление представляется таким образом: прямые лучи падают на мельчайшие неоднородности среды, от которых по всем направлениям (включая и направление, обратное падающему свету) расходятся лучи рассеянного света, значительно более слабые по интенсивности (рис. 4, б).

Рассеяние света в газе

Рассеяние света происходит также в среде чистого газа (например, атмосферного воздуха) около центров колебаний (флюктуации) плотности газа, происходящих в результате беспорядочного теплового движения молекул газа. Этот вид рассеивания называется молекулярным.

Интенсивность рассеяния зависит от длины волны света: короткие волны рассеиваются значительно сильней, чем длинные. Интенсивность I_рас рассеянного света в дисперсных средах с размерами неоднородностей, меньшими длины волны, обратно пропорциональна примерно четвертой степени длины волны (закон Рэлея).

Вследствие рассеяния в атмосфере преимущественно коротких волн цвет неба представляется нам сине-голубым, а прямое солнечное излучение приобретает желто-красный оттенок, особенно при восходе и заходе солнца, когда оно проходит более длинный путь в атмосфере.

Интенсивность света, рассеянного на относительно крупных частицах, обратно пропорциональна этой степени длины волны. Поэтому, например, мелкодисперсный туман имеет синий цвет, а состоящий из более крупных капелек — белый.

Рассеяние света происходит также на мельчайших неровностях (шероховатостях) поверхности раздела, различных по оптическим свойствам сред (рис. 4, в). Такие поверхности называются матовыми, а само явление — поверхностным рассеянием или диффузным отражением. Интенсивность рассеянного света в этом случае обратно пропорциональна второй степени длины волны. Коэффициент диффузного отражения от поверхностей называется альбедо.

Статья на тему Дифракция