ЭНЕРГИЯ ЭЛЕКТРИЧЕСКОГО ПОЛЯ

При включении цепи, состоящей из сопротивления r и емкости С (рис. 4-7), на постоянное напряжение U в цепи возникает ток и происходит зарядка конденсатора.

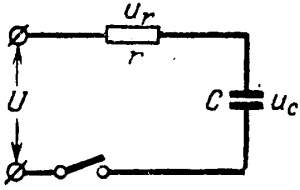
Напряжение на зажимах цепи в каждый момент времени будет состоять из двух слагающих

U = u_r + u_c

где u_r = i_r — напряжение на сопротивлении r; и_с = q/C — напряжение на обкладках конденсатора. Умножив написанное уравнение на idt получим

Рис. 4-7. Цепь с сопротивлением и емкостью.

Uidt = i²r dt + u_cidt = i²rdt + u_cCdu_c

Левая часть уравнения представляет собой энергию, получаемую цепью за время dt, от источника питания. Первая слагающая правой части i²r dt — энергия, переходящая за время dt в тепло в сопротивлении r, а вторая слагающая

dW_c =и_сС du_c

представляет собой энергию, запасаемую в электрическом поле при возрастании напряжения на конденсаторе на величину du_c. Так как произведение u_cC = q, то

dW_c = q du_c.

Заряд конденсатора q растет пропорционально напряжению и графически выражается прямой, проходящей через начало координат (рис. 4-8). Энергия, полученная конденсатором при возрастании напряжения на его зажимах на du_c, выразится заштрихованной площадкой (рис. 4-8). Вся энергия, накопленная конденсатором в его электрическом поле при возрастании напряжения от нуля до и_с, выразится суммой таких площадок, т.е. площадью треугольника OAБ. Таким образом, энергия электрического поля

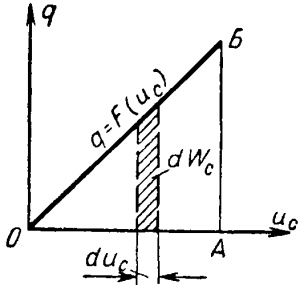
Рис. 4-8. График за ряда конденсатора q = f (и_с).

Энергия, накопленная в электрическом поле конденсатора при его включении, выделяется при распаде электрического поля.

Пример 4-2. Определить энергию, запасенную в электрическом поле

конденсатора емкостью 50 мкф, если напряжение на конденсаторе 300 в. Энергия электрического поля

Статья на тему Энергия электрического поля

• ← Предыдущая
• Следующая →
• Главная Электротехника