Электромагнитная индукция это возбуждение электродвижущей силы в проводнике под действием магнитного поля называется электромагнитной индукцией. Электромагнитная индукция происходит, например, при движении проводника в магнитном поле с постоянной напряженностью или при изменении напряженности поля, в котором находится неподвижный проводник.
Электродвижущая сила наведенная в проводе
Во всяком проводе, который при движении в магнитном поле пересекает магнитные линии, возбуждается электродвижущая сила, получившая название э. д. с. электромагнитной индукции, а само явление — электромагните ной индукцией.
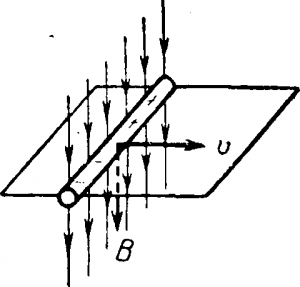
На рис. 3-13 показан провод, движущийся с постоянной скоростью и, в однородном поле, перпендикулярно магнитным линиям.
При движении провода с той же скоростью υ будут перемещаться свободные электроны и положительные ионы провода. Следовательно, на каждую заряженную частицу будет действовать электромагнитная сила, направление которой определяется по правилу левой руки. Электромагнитные силы вызовут перемещение электронов на один конец провода, создавая на нем отрицательный заряд. На другом конце провода недостаток электронов вызовет положительный заряд. Разделение зарядов закончится если электромагнитные силы уравновесятся силами электрического поля разделенных зарядов.
Разность потенциалов на концах разомкнутого провода, движущегося в магнитном поле, равна э. д.с. электромагнитной индукции. Согласно (1-3) э. д. с. на концах провода длиной l:
E = ؏l
Напряженность электрического поля в проводе
؏ = F : q
а сила, действующая на электрон, F = Bυq, следовательно,
Е = Bυl,
таким образом, наведенная э. д. с. равна произведению магнитной индукции поля, длины провода и скорости его движения в направлении, перпендикулярном магнитным линиям.
Направление наведенной э. д. с. определяется по правилу правой руки: ладонь правой руки располагают так, чтобы магнитные линии входили в нее, отогнутый под прямым углом большой палец совмещается с направлением движения проводника, тогда вытянутые четыре пальца укажут направление наведенной э. д. с. (рис. 3-14).
Рис. 3-14. Правило правой руки.
При определении наведенной э. д. с в проводнике, движущемся в плоскости, расположенной под углом α к вектору магнитной индукции поля, следует брать слагающую скорости, перпендикулярную к вектору магнитной индукции, т. е. υH = υ sin α.
Движение проводника вдоль магнитных линий (v cos а) не вызывает появления электромагнитных сил. Таким образом, э. д. с.
E = BlυH = Blυ sinα
Если провод движется в плоскости, перпендикулярной магнитным линиям поля, перемещаясь на расстояние ∆bза время ∆t, то наведенная в нем э. д. с.
E= BlυH = Bl(∆b:∆t)
Так как произведение магнитной индукции В и площади ∆S = l∆b равно магнитному потоку ∆Ф = B∆S, пересеченному проводом при его движении, то наведенная в проводе э. д. с.
Таким образом, наведенная в проводе э. д. с. равна скорости пересечения проводником магнитного потока.
Электродвижущая сила наведенная в контуре
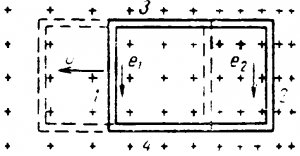
Определим э. д. с. наведенную в контуре (рис. 3-15), который движется в неоднородном поле, магнитные линии которого (показаны крестиками) перпендикулярны плоскости контура.
При движении контура в направлении указанном стрелкой, стороны его 3 и 4 не пересекают магнитных линий и, следовательно, в них не наводятся э. д. с. В сторонах 1 и 2 контура наводятся э. д. с. е1 и е2, направления которых, найденные по правилу правой руки, показаны стрелками.
Рис. 3-15. Движение контура в магнитном поле.
Величины э. д. с.:
e1 = ∆Ф1 : ∆t и e2 = ∆Ф2 : ∆t
где ∆Ф1 и ∆Ф2 — потоки, пересеченные сторонами 1 и 2 контура за время ∆t. Сторона 1 пересекает поток ∆Ф1, который входит в контур, а сторона 2 пересекает ∆Ф2, который выходит за пределы контура. При заданном направлении магнитного потока согласно правилу буравчика направление е2 будет положительным, а е1 — отрицательным, следовательно, наведенная в контуре э. д. с.
е = е2 — е1 = (∆Ф2 — ∆Ф1 ): ∆t
Обозначив поток, пронизывающий контур до его движения, через Ф1 а по прошествии времени ∆t через Ф2(положение контура показано пунктиром), получим:
Ф2 = Ф + ∆Ф1 — ∆Ф2.
Приращение потока, пронизывающего контур за время ∆t:
∆Ф = Ф2 — Фх = ∆Ф1 — ∆Ф2,
или
∆Ф2 — ∆Ф1 = — ∆Ф, а наведенная в контуре э. д. с.
e = — ∆Ф : ∆t
Эта формула дает среднее значение э. д. с. за время At. Для определения величины э. д. с. в произвольный момент времени надо найти приращение потока dФ за бесконечно малый промежуток времени dt и написать:
e = dФ : dt
Выражения показывают, что необходимым условием возникновения в контуре э. д. с. является изменение магнитного потока, пронизывающего контур.
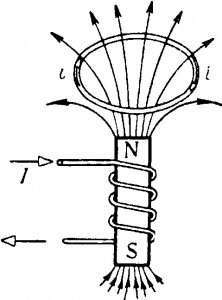
Рис. 3-16. Ток, индуктированный в кольце.
Если контур состоит не из одного витка, а из w витков, соединенных последовательно, т. е. представляет собой катушку, то индуктированная в ней э. д. с. будет в ɯ раз больше, чем в одном витке, т. е.
е = ɯ(dФ : dt)
Произведение из числа витков на пронизывающий их магнитный поток называется потокосцеплением и обозначается буквой Ψ:
Ψ = ɯФ,
следовательно э. д. с.
е = — (dФ : dt) = —(dΨ : dt)
т. е. индуктированная в катушке э. д. с. равна скорости уменьшения потокосцепления.
При движении контура в направлении, указанном на рис. 3-15, приращение магнитного потока контура отрицательно, так как ∆Ф2 > ∆Ф1 и ∆Ф < 0, т. е. поток, пронизывающий контур, уменьшается. Следовательно, согласно э. д. с. будет положительной и направлена по направлению движения часовой стрелки, будет положителен и направлен, так же как и э. д. с, вызванный ею ток в контуре.
Этот ток создает магнитный поток, который по правилу буравчика будет иметь то же направление, что и убывающий магнитный поток. Таким образом, убывание потока, пронизывающего контур, приводит к появлению э. д. с. и тока такого направления, который стремится компенсировать уменьшение потока, сцепленного с контуром.
При движении контура в обратном направлении ∆Ф > О и э. д. с. согласно будет, отрицательна и направлена против движения часовой стрелки, будет отрицательным и направлен так же, как и э. д. с, вызванный ею ток, а созданный током магнитный поток будет направлен противоположно возрастающему магнитному потоку контура. Таким образом, возрастание потока контура приводит к появлению э. д. с. и тока, который своим магнитным потоком стремится компенсировать увеличение потока контура.
Из рассмотренного можно сделать вывод: если причиной наведения э. д. с. является изменение магнитного потока, пронизывающего контур, то наведенная э. д. с. будет направлена так, что вызванный ею ток будет препятствовать изменению потока контура.
Это положение было установлено в 1833 г. русским академиком Э. X. Ленцем и называется законом Ленца: направление наведенной э. д. с. таково, что вызванный ею ток противодействует причине появления э. д. с.
На рис. 3-16 изображена катушка с сердечником, над которой расположено металлическое кольцо. При увеличении тока в катушке или при сближении кольца и катушки увеличивается магнитный поток, пронизывающий кольцо, и в нем наводится э. д. с. и проходит ток. Согласно закону Ленца направление магнитного потока, созданного током i в кольце, противоположно направлению потока катушки. Применив правило буравчика, легко определить направление индуктированного тока i.
Что такое электромагнитная индукция
Электромагнитную индукцию можно показать с помощью двух катушек А и Б (рис.) Катушка А имеет железный сердечник и через ключ К и реостат Р подключена к источнику Б постоянного напряжения. Катушка Б соединена с гальванометром Г с нулем посредине шкалы. Если замкнуть цепь тока в катушке А и таким образом создать в ней магнитное поле, а затем катушку Б надвинуть на катушку Л, то стрелка гальванометра покажет наличие в цепи кратковременного тока. При раздвижении катушек стрелка отклонится в обратную сторону Если катушки сближать быстрее, то отклонение стрелки будет больше, и наоборот
Во втором опыте катушка Б надвинута на катушку А, но ток в катушке А выключается и выключается ключом К или постепенно изменяется с помощью реостата Р Соответственно изменяется и магнитное поле, создаваемое в катушке А При каждом изменении поля гальванометр Г отмечает появление в катушке Б тока, направление которого связано с характером изменения поля (усиление или ослабление), а сила тока зависит от скорости этого изменения.
Электромагнитная индукция происходит только при условии, что оси катушек совпадают. Если они расположены взаимно перпендикуляр индукции не происходит. Однако индукцию вновь можно наблюдать в процессе поворота одной из катушек относительно другой.
Индукцию можно наблюдать также при вращении катушки или витка в постоянном магнитном поле или при изменении площади витка. Заметим, что первичным при электромагнитной индукции является возникновение в контуре электродвижущей силы. Если контур замкнут, то в нем образуется также и индукционный ток.
Для обобщения условий, при которых происходит электромагнитная индукция, вводят представление о магнитном потоке, через площадь данного контура. При достаточно однородном магнитном поле и площади контура, перпендикулярной силовым линиям поля, магнитный поток численно равен произведению магнитной индукции В на площадь 5 контура:
Ф = ВS.
Если линии магнитной индукции В образуют с перпендикуляром к площади контура угол ер, то в выражение для магнитного потока входит проекция В’ вектора магнитной индукции на направление этого перпендикуляра:
Ф = В’S= ВScos φ.
Единицей измерения магнитного потока в системе СГС является максвелл (мкс): 1 мкс = 1 э•см2. В системе СИ — вебер (вб).
Рассматривая все возможные условия, при которых происходит электромагнитная индукция, можно установить, что при этом изменяется или величина магнитной индукции, или площадь контура, через которую линии индукции проходят, т. е. в обоих случаях имеет место изменение потока магнитной индукции через площадь контура.
Таким образом, явление электромагнитной индукции заключается в том, что при изменении магнитного потока через площадь контура проводника в последнем возникает э. д. с. индукции. Электродвижущая сила индикции прямо пропорциональна скорости изменения магнитного потока и не зависит от условий, вызывающих это изменение (закон Фарадея).
Явление электромагнитной индукции
В основе электромагнитной индукции лежит действие магнитного поля на движущиеся заряды, т. е. силы Лоренца. Концы подвижной рамки Р подключим к гальванометру Г и вытолкнем посторонней силой сторону аb рамки из межполюсного пространства магнита М в том же направлении, в котором она двигалась в опыте.. При этом стрелка гальванометра отклонится в сторону, противоположную первому опыту. Следовательно, в проводнике аb рамки Р возникла э. д. с. индукции, вызвавшая в рамке ток, обратный по направлению току в предыдущем случае.
Для выяснения механизма индукции сравним опыты. Проводник А Б находится в магнитном поле. В первом случае движение зарядов вдоль проводника происходит под действием приложенного напряжения. Силы Лоренца, действуя на заряды, выталкивают проводник. Во втором случае заряды вместе с проводником перемещаются внешней силой в том же направлении (вектор скорости υ). Силы Лоренца, действуя на заряды в направлении, перпендикулярном их движению, т. е. вдоль проводника, вызывают разделение в нем зарядов и как следствие — образование на его концах разности потенциалов, которая и является э. д. с. индукции.
В обоих случаях направление силы Лоренца определяется по правилу левой руки, только во втором случае за направление тока принимается направление движения проводника (заметим, что в обоих случаях рассматривается условное направление тока; движение электронов, показанное стрелками внутри проводника А Б, происходите противоположном направлении).
Направление электродвижущей силы индукции или индукционного тока определяется правилом Ленца: направление наведенных электродвижущих сил, токов и создаваемых ими магнитных полей таково, что они всегда противодействуют причине, вызывающей индукцию.
Определим величину электродвижущей силы индукции, которая наводится в одиночном контуре или витке. По закону Фарадея величина ее прямо пропорциональна скорости изменения магнитного потока через площадь контура. Пусть в начальный момент t1 магнитный поток имел значение Ф1 и к моменту t2 его значение стало Ф2.
Это означает, что за время ∆t = t.2 —t1 произошло изменение магнитного потока на величину ∆Ф = Ф2—Ф1 Отношение изменения магнитного потока к соответствующему промежутку времени ∆Ф/∆t— при достаточно малом ∆t характеризует скорость изменения магнитного потока. Следовательно, обозначив электродвижущую силу индукции через Ei, запишем, что
Знак минус в формуле отражает правило Ленца: при увеличении магнитного потока (∆Ф/∆t ) > 0 э. д. с. индукции отрицательна, т. е. направлена против часовой стрелки, если смотреть вдоль направления силовых линий поля; при уменьшении магнитного потока (∆Ф/∆t) < 0 э. д. с. индукции положительна, т. е. направлена по часовой стрелке, при тех же условиях наблюдения.
Коэффициент k зависит от выбора единиц. В системе СИ k=1, тогда Et = — ∆Ф/∆t. С помощью этой формулы определяется единица магнитного потока вебер.
Если принять Et = 1 в и ∆t =1сек, то ∆Ф будет равняться 1 вб. Отсюда вебер определяется как магнитный поток через замкнутый контур, который при равномерном убывании до нуля в течение 1 сек индуцирует в контур, электродвижущую силу в 1 в (1 вб =1 в•сек).
Теперь можно дать единице магнитной индукции тесла следующее определение: тесла есть магнитная индукция такого однородного поля, в котором магнитный поток через площадку в 1 ж2, перпендикулярную направлению поля, равняется 1 вб (1 тл = 1вб1м2); 1 тл =104 гс. Этому определению тесла соответствует размерность магнитной постоянной гн/м.
Здесь заметим, что размерности тесла вб/м2 и н/а•м соответствуют друг другу: вб/м2=в•сек/м2=вт•сек/(а• м2) =дж/(а• м2) = н/а м.
Если магнитный поток выражен в единицах системы СГС — максвеллах, то k =10-8и формула для электродвижущей силы индукции принимает вид:
Ei = — 10-8 (∆Ф/∆t). Следовательно, 1 вб=108 мкс.
Если, индукция происходи г в катушке из п витков, то электродвижущая сила (так как п витков в катушке соединены последовательно) всей катушки будет в п раз больше:
Ein = — kn(∆Ф/∆t).
Статья на тему Электромагнитная индукция



Добавить комментарий
Для отправки комментария вам необходимо авторизоваться.