ВЕКТОРНАЯ ДИАГРАММА
Синусоидальные величины изображают или синусоидами, или вращающимися векторами.
Такое изображение дает возможность найти амплитуду, начальную фазу и период, т. е. все величины, определяющие синусоидальную величину.
При изображении синусоидальной величины вращающимся вектором длина вектора в определенном масштабе представляет собой амплитуду величины; угол между вектором и положительным направлением оси абсцисс в начальный момент равен начальной фазе, а угловая скорость вращения вектора равна угловой частоте. Мгновенное значение синусоидальной величины, представленной вращающимся вектором, определяется проекцией вектора на ось ординат.
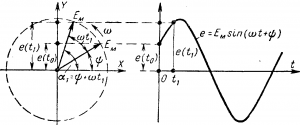
Например, для изображения э. д. с. е = Eмsin (ωt + Ψ) под углом Ψ к положительному направлению оси абсцисс (рис. 5-9) проводят вектор в выбранном масштабе, выражающий амплитуду Ем.
Рис. 5-9. Изображение синусоидальной величины вращающимся вектором.
При вращении вектора в положительном направлении (рис. 5-9) с угловой скоростью со проекции его на ось ординат (ось Y) выражают для соответствующих моментов времени мгновенные значения э. д. е., так как они в выбранном масштабе представляют величины
Ем sin α = Eм sin (ωt + Ψ)
Ha графике (рис 5-9) для момента времени t1 э. д. с. изображена ординатой e (t2), равной проекции на ось Y вращающегося
вектора, расположенного в этот момент под углом α = (ωt1 + Ψ) к оси абсцисс.
Один или несколько векторов, изображающих синусоидальные величины одной частоты, называются векторной диаграммой.
При вращении векторов, образующих векторную диаграмму, взаимное расположение их остается неизменным. Обычно интересным является сдвиг фаз между отдельными величинами. Поэтому при построении векторной диаграммы вектор, который проводится первым, направляют произвольно, а остальные векторы диаграммы располагают по отношению к нему под углами, равными углам сдвига фаз.
Рис. 5-10. Сложение двух векторов э. д. с.
Векторные диаграммы широко применяются при рассмотрении явлений в цепях переменного тока.
На рис. 5-10 показаны два вектора э. д. с. Ем1 и Ем2 и геометрическая сумма их — вектор суммарной э. д. с. Ем в момент времени t = 0, Для любого момента времени
сумма проекций вращающихся векторов Eм1 и Ем2 на ось У равна проекции на ту же ось суммарного вектора Емт. е. е = е1 + е2 так как взаимное расположение векторов при их вращении не изменяется. При сложении двух синусоидальных величин одной частоты получается синусоидальная величина той же частоты, амплитуда которой выражается длиной суммарного вектора, например:
Ēм = Ēм1 + Ēм2
Черточки над буквами указывают на то, что величины являются векторами и, следовательно, сложение их производится геометрически по правилу параллелограмма (треугольника).
Вычитание двух синусоидальных величин выполняется как сложение уменьшаемой величины с обратной по знаку вычитаемой величиной, т. е.
е1 — е2 = е1 + (—е2)
Статья на тему Векторная диаграмма