Что такое вязкость и ламинарное течение жидкости
Силы взаимного притяжения имеются не только между молекулами самой жидкости, но также между молекулами жидкости и твердых тел, с которыми жидкость соприкасается, например стенок сосуда, в котором юна находится, или трубы, по которой она протекает.
Если эти силы больше сил, действующих между молекулами самой жидкости, то жидкость прилипает к стенке или ее смачивает. В этом случае при течении жидкости прилегающий к стенке слой молекул остается неподвижным. Остальная масса жидкости разделяется на молекулярные слои, двигающиеся с постепенно возрастающими от слоя к слою скоростями. Такое течение жидкости называется ламинарным.
Что такое ламинарное течение жидкости
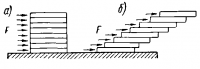
Для пояснения ламинарного течения жидкости рассмотрим сугубо схематическую модель, состоящую из стопки тонких однородных пластинок, расположенных на неподвижной плоскости П, на каждую из которых действуют равные, одинаково направленные силы F (рис. 2, а). Под действием силы F каждая из пластинок будет, преодолевая трение, смещаться относительно нижележащей пластинки. Однако сама нижележащая пластинка при этом смещается относительно еще более нижележащей и т. д В результате пластинки смещаются относительно исходного положения неравномерно: верхние больше, чем нижние, и через некоторое время стопка принимает вид, показанный на рис. 2, б.
Нечто подобное происходит и при ламинарном течении вязкой, смачивающей стенки сосуда жидкости. Постоянное по величине давление вызывает скольжение соприкасающихся слоев молекул жидкости один относительно другого. В результате центральные слои двигаются со значительно большей скоростью, чем периферические. Общеизвестно, например, что течение реки в средней части быстрее, чем у дна и стенок русла.
При ламинарном течении жидкости по трубе постоянного сечения скорость движения слоев молекул постепенно увеличивается от периферии к оси трубы. Однако при этом разность между скоростями двух соседних слоев имеет наибольшую величину у стенок трубы и постепенно уменьшается к центру ∆υ’ >∆υ» (рис. 3, а). Если концы векторов скорости соединить плавной кривой, то получится кривая, называемая в математике параболой.
Опыт с жидкостью
Это можно показать на следующем опыте. Наполним стеклянную трубку с краном на две трети бесцветной вязкой жидкостью, например глицерином, сверху нальем такую же, но подкрашенную жидкость так, чтобы между ними была видна резкая горизонтальная граница. Если открыть кран и дать жидкости вытекать из трубки, то вследствие большей скорости движения центральных слоев жидкости по сравнению с пристеночными граница постепенно изменяет форму и делается все более и более вытянутой вниз в средней части.
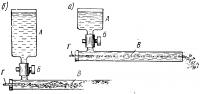
Характер течения жидкости можно наблюдать также при помощи следующего прибора (рис. 4). Стеклянная трубка В соединена с резервуаром А, заполненным чистой водой. В трубку с торца вставлен стержень Г из легко-растворяющейся краски. При движении из резервуара А вода растворяет конец стержня Г и в общий ток воды вступает окрашенная струйка. По картине дальнейшего движения этой струйки можно судить о характере движения частиц в общем потоке жидкости.
Скорость движения воды в трубке можно регулировать краном Б. При сравнительно небольшой скорости движения окрашенная струйка не смешивается с основным потоком (рис. 4, а) — течение имеет ламинарный характер. Ламинарное течение жидкости происходит при небольших скоростях движения в трубах с относительно гладкими стенками, без резких изменений площади сечения или направления течения, а также при отсутствии множественных разветвлений.
Турбулентное течение
Если в нашем опыте увеличить скорость движения воды, то окрашенная струя начинает колебаться, теряет резкую границу, образует завихрения и при еще большей скорости разрывается и смешивается с общим потоком воды (рис. 4, б). Это связано с тем, что при значительной разнице в скоростях пристеночных и центральных слоев в этих слоях появляется разница в давлении жидкости (правило Бернулли). В связи с этим частицы жидкости из периферических слоев, где давление выше, переходят в центральные слои, где давление меньше, в результате чего и образуются завихрения. Подобное течение жидкости называется турбулентным.
Турбулентное течение возникает при высоких скоростях течения, а также при резких сужениях просвета, значительной шероховатости стенок или в местах множественного разветвления русла или трубы, по которой течет жидкость. Для него характерны звуковые явления (шум, журчание и т. п.), возникающие вследствие образующегося при этом колебательного движения частиц жидкости.
Измерение вязкости жидкости
Ламинарное течение жидкости используется для измерения внутреннего трения или вязкости жидкости. Рассмотрим силу трения, возникающую между двумя параллельными соприкасающимися слоями жидкости, двигающимися со скоростями υ1 и υ2.
Разность скоростей ∆υ=υ2 — υ1, отнесенная к расстоянию х между осями соответствующих слоев жидкости: ∆υ\х = (υ2 — υ1)/х или разность скоростей, приходящаяся на единицу расстояния между слоями жидкости, называется градиентом скорости в направлении, перпендикулярном оси трубы (градиентом какой-либо физической величины называется изменение ее, приходящееся на единицу расстояния, вдоль которого это изменение рассматривается).
По формуле Ньютона сила F внутреннего трения между двумя слоями жидкости прямо пропорциональна площади S их соприкосновения и градиенту скорости ∆υ\х между этими слоями:
F = η(∆υ\х)S
где коэффициент пропорциональности η зависит от природы жидкости (также и от ее температуры) и называется коэффициентом внутреннего трения или коэффициентом вязкости жидкости
Если ∆υ\х =1 и S = 1, то η = F следовательно, коэффициентом вязкости называется величина численно равная силе трения, возникающей при ламинарном течении между двумя слоями жидкости, соприкасающихся па площади, равной единице, при градиенте скорости между ними, также равном единице.
Единицей измерения коэффициента вязкости в системе СИ является н•сек/м2, в системе СГС — дин сек•см2, эта единица называется пуазом (nз): 1 н•сек/м2=10 пз.
С повышением температуры коэффициент вязкости значительно снижается. Это связано с тем, что при повышении температуры силы притяжения между молекулами жидкости (вследствие увеличения расстояния между ними) уменьшаются.
Непосредственное измерение силы трения между слоями жидкости затруднительно. Поэтому вязкость жидкости определяют косвенно путем наблюдения или скорости ее течение в капиллярной трубке (способ капиллярного вискозиметра) или скорости падения в ней небольших тел сферической формы (способ Стокса). При этом для упрощения задачи путем сравнительных измерений находят относительную вязкость данной жидкости ηотн, под которой понимают отношение коэффициентов вязкости данной жидкости η и воды. Тогда, зная, что вязкость воды при 20°С равняется 0,01 пз, можно найти коэффициент вязкости заданной жидкости: η =0,01ηотн.
Определение вязкости
Определение вязкости методом капиллярного вискозиметра основано на том, что согласно формуле Гагена — Пуазейля объем V вязкой жидкости, протекающий по тонкой трубке за определенный промежуток времени, при прочих равных условиях (в частности, при одинаковой температуре) обратно пропорционален коэффициенту вязкости ч\ жидкости. Следовательно, для двух сравниваемых жидкостей коэффициенты вязкости обратно пропорциональны объемам:
η1/η2 = V2/V1
Применяемый в клинике прибор для определения вязкости крови состоит из двух градуированных пипеток А к Б, укрепленных на общей подставке П. В средней части пипеток имеются одинаковые капилляры а и б. Слева концы пипеток соединены тройником В, от которого идет резиновая трубка Д со стеклянным наконечником Е. Нижняя пипетка имеет слева разобщительный кран Г. При измерении, открыв кран Г и втягивая ртом воздух через наконечник E, наполняют пипетку Б водой до метки 0.
Затем, закрыв кран Г, аналогичным образом наполняют до такого же уровня пипетку А исследуемой кровью (все исследование должно производиться быстро, чтобы кровь не успела свернуться). Затем открывают кран Г и, энергично втягивая ртом воздух, всасывают жидкости из обеих пипеток так, чтобы кровь дошла до цифры 1. При этом вода как менее вязкая жидкость дойдет до более высокой цифры, которая и укажет относительную вязкость крови.
При наличии больших количеств жидкости определение коэффициента вязкости может быть сделано методом Стокса. Стоке эмпирически установил, что при не слишком быстром движении тела сферической формы в вязкой жидкости сила FB сопротивления движению прямо пропорциональна скорости υ, радиусу r тела и коэффициенту вязкости ηжидкости: FB = 6πrηυ.
Если небольшой шарик радиуса r из вещества с плотностью ρ свободно падает в жидкости с плотностью ρ1 то в случае его равномерного движения можно считать, что три действующие на него силы: сила тяжести (Р = (4/3)πr3ρg), выталкивающая сила (Q = (4/3)πr3ρ1g) и сила сопротивления FB взаимно уравновешиваются:
Р = Q + FB, откуда FB = Р — Q или 6πrηυ = (4/3)πr3g (ρ — ρ1). Отсюда коэффициент вязкости жидкости:
η = (2/9)gr2((ρ — ρ1)/υ)
Для измерения берут высокий узкий цилиндр, в средней части которого имеются две метки а и Ь и набор металлических шариков диаметром 0,2—0,3 мм. Цилиндр заполняют исследуемой жидкостью. Затем берут шарик, опускают его в жидкость по оси цилиндра и наблюдают по секундомеру за его падением.
При прохождении шариком первой метки секундомер запускают, при прохождении второй — останавливают. Зная расстояние h между метками и время падения шарика, вычисляют его скорость υ. Радиус шарика определяют, пользуясь микроскопом с небольшим увеличением и окулярной шкалой. Коэффициент вязкости исследуемой жидкости находится из предыдущего соотношения.
Статья на тему Вязкость