Что такое кристаллографические символы Закон рациональных отношений
Многообразие внешнего облика кристаллов, встречающихся в природе, обусловлено различными сочетаниями, или комбинациями, простых форм.
Определив элементы симметрии кристалла, количество простых форм и вид симметрии кристалла, не всегда получают однозначное представление о кристалле.
Один класс симметрии может включать в себя несколько различных по внешнему виду кристаллов.
Например, кристаллы кварца могут встречаться в виде гексагональной дипирамиды или комбинации гексагональной дипирамиды с гексагональной призмой.
Разные по внешнему виду оба кристалла имеют одинаковую формулу симметрии:
L66L27PC.
То же можно сказать о кристаллах циркона.
Все четыре формы относятся к одному и тому же виду симметрии тетрагональной сингоний:
L44L25PC.
А кристаллы под номерами 4 и 5 даже состоят из одних и тех же простых форм — двух тетрагональных призм и тетрагональной дипирамиды.
Таким образом, определение вида симметрии или даже наличие стереографической проекции кристалла не всегда дает нам однозначное представление о внешнем облике кристалла.
Для более точной характеристики кристалла определяют взаимное расположение его граней в пространстве по отношению к определенным координатным осям и некоторой исходной грани.
Для определения грани применяются так называемые кристаллографические символы.
Понятие о кристаллографических символах вытекает из второго закона кристаллографии, открытого в 1784 г. французским исследователем Р. Ж. Гаюи.
Этот закон называется законом рациональных отношений или законом параметров, именуемым также законом целых чисел.
Закон рациональных отношений гласит: положение всякой грани может быть определено тремя целыми числами.
Если за оси координат выбраны направления трех ребер кристалла и за единицы измерения взяты отрезки, отсекаемые на этих осях одной из граней кристалла.
Нередко дается и другая формулировка данного закона — «двойные отношения параметров (отрезков), отсекаемых двумя любыми гранями кристалла на трех пересекающихся его ребрах, равны отношениям целых и сравнительно малых чисел» .
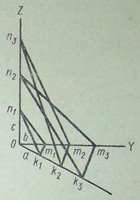
Возьмем три непараллельных ребра кристалла, пересекающихся в точке О, и обозначим их ОХ, ОУ, OZ. Выбранные три ребра примем за координатные оси (рис.).
Покажем три грани кристалла, пересекающие координатные оси:
R1m1n1, R2m2n3 и R3m3n2
Отрезки, отсекаемые этими гранями на осях, называются параметрами граней. Например, для грани R1m1n1 параметрами являются OR1, Om1 и Оn1.
Примем параметры этой грани за единицы измерения по соответствующим осям (Ok1 — по оси X, Om1 — по оси Υ, Оn1 — по оси Z). В этом случае параметры остальных граней кристалла будут рациональными числами.
Выбранная грань называется единичной гранью, а ее параметры — осевыми единицами. Эти осевые единицы взяты за единицы измерения — единичные отрезки.
Следует иметь в виду, что эти параметры могут быть не равны друг другу (например, на рис. у грани k1m1n1 параметры ОƦ1≠Оm1≠Оn1).
Положение данной грани обозначается символом (111). Символ обозначает, что грань отсекает по каждой оси по одной осевой единице.
В кристаллографии принято так располагать кристаллографические оси:
X — на себя — положительное значение, от себя — отрицательное;
Υ — вправо — положительное значение, налево — отрицательное,
Z — вверх — положительное значение, вниз — отрицательное.
Осевые единицы обозначают: по X — а, по Υ — b, по Z — с.
Выбор единичной грани задаст масштаб по каждой оси. В нашем случае при выбранной единичной грани K1m1n1 ее параметрами будут а, b, с.
Положение грани Ʀ2m2n3 определится параметрами 2а, 2b, 3с, для грани Ʀ3m3n2 — 3а, 36, 2с.
Чтобы представить положение каждой грани в пространстве, следует знать (помимо направления осей), как параметры, задающие масштабы по разным осям, относятся друг к другу.
В общей форме отношение параметров любой грани можно выразить как ра:qb : rc, где р, q и r — целые числа.
Для каждого определяемого кристалла необходимо выбрать направление кристаллографических осей и одну из наклонных к ним граней в качестве единичной грани. Эту операцию называют установкой кристалла.
Иногда при установке кристалла некоторые грани оказываются параллельными одной или двум координатным осям.
В этом случае их параметры по данным осям будут равны бесконечности (∞). Для примера обозначений граней кристалла приведем куб с указанием символов всех его граней (рис. 2).
При описании кристаллов и определении символов получают для каждой простой формы или комбинации простых форм совокупность символов многих граней.
Например, для куба символы всех его шести граней: (100), (010), (001), (100),(010) и (001).
Принято для обозначения каждой простой формы брать символ одной из ее граней, для которой характерно наибольшее количество положительных индексов.
| Таблица 3 Символы простых форм кубической сингонии |
||
|
Название простой формы
|
Символ
|
Количество граней
|
|
Гексаэдр (куб)
Октаэдр
Тетраэдр
Ромбододекаэдр
Пентагон-додекаэдр
Тетрагексаэдр
Гексоктаэдр
|
{1 0 0}
{1 1 1}
{1 1 1}
{1 1 0}
{h Ʀ 0}
{h Ʀ 0}
{h Ʀl}
|
6
8
4
12
12
24
48
|
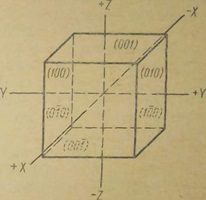
пунктиром показаны символы невидимых граней
Такие символы, условно относящиеся к той или иной простой форме, принято заключать в фигурные скобки.
В нашем случае для куба, являющегося простой формой, вместо приведенных выше шести символов употребляют лишь один символ {100}.
В табл. 3 приведены символы наиболее распространенных простых форм кубической сингонии.
Установка кристаллов. Константы кристаллической решетки
Для построения наглядных стереографических проекций и определения символов граней кристаллов разных сингонии применяют установку кристаллов.
Под установкой кристаллов понимают выбор определенных направлений за координатные оси и одной из наклонных к ним граней кристалла за единичную.
Обычно координатные оси проводятся параллельно ребрам и часто по осям симметрии кристалла и называются кристаллографическими осями.
При установке кристаллов и выборе координатных осей следует иметь в виду, что углы между кристаллографическими осями могут отличаться от 90° в зависимости от принадлежности кристалла к той или иной сингонии.
Принято осевые углы обозначать буквами греческого алфавита: а (угол между осями Y и Z), р (угол между осями X и Z) и у (угол между осями X и Y) (рис. 3).
Отношение осевых единиц а : b : с и осевые углы α, β и γ называются константами данной кристаллической решетки.
К наиболее простой относится установка кристаллов высшей категории — кубической сингонии (см. рис. 2).
Здесь кристаллографические оси устанавливаются вдоль осей симметрии четвертого порядка или, в случае их отсутствия, по осям второго порядка.
Все три кристаллографические оси будут взаимно перпендикулярны, т. е. α=β=γ=90°.
| Константы кристаллической решетки Таб. 3 | ||
| Сингонии | Осевые единицы | Осевые углы |
|
Кубическая
Гексагональная
Тригональная
Тетрагональная
Ромбическая
Моноклинная
Триклинная
|
α=b = С
α= b≠с
α=b≠с
α =b≠с
α≠b≠с
α≠b≠с
α≠b≠с
|
α = β = γ = 90°
α= β = 90 ° γ= 120°
α= β = 90°γ = 120°
α = β = γ = 90°
α =β = γ = 90°
α = γ= 90°β≠90°
α ≠ р ≠ β≠90°
|
За единичную грань принимают грань тетраэдра или октаэдра, символ которых будет (1 1 1).
Осевые отрезки, отсекаемые на кристаллографических осях, равны между собой: α=b = с.
Ось Z располагается вертикально, оси X и Z — горизонтально.
Причем положительное значение оси X направляется на наблюдателя, положительное значение Y — слева направо.

В триклинной сингонии кристаллографические оси проводятся параллельно трем произвольно выбранным ребрам, ее лежащим в одной плоскости (рис. 45, 1).
За единичную грань берут любую грань, пересекающую координатные оси. У нас получается косоугольная система координат, где α≠β≠γ≠90°, а осевые единицы: α≠b≠с.
В моноклинной сингонии ось У проводится параллельно оси второго порядка, а при ее отсутствии — перпендикулярно к плоскости симметрии. Ось Z проводится вертикально и перпендикулярно к оси Y.
Ось X проводится перпендикулярно к оси Y, положительный конец оси X направлен на наблюдателя и наклонен вниз (рис. 4,2).
Здесь мы имеем: α=γ=90°, β≠90°, α≠b≠с. За единичную грань принимают любую грань, пересекающую все три кристаллографические оси.
В ромбической сингонии кристаллографические оси проводятся через три взаимно перпендикулярные оои симметрии второго порядка.
При наличии одной оси симметрии второго порядка через нее проводят ось Z. Две другие оси в этом случае проводятся перпендикулярно к плоскости симметрии.
За единичную грань принимают любую грань, пересекающую все три кристаллографические оси. При установке кристалла ось X направляют на наблюдателя, ось Y— слева направо (рис. 4,3).
Для ромбических кристаллов α=β=γ=90°, следовательно, это прямоугольная система координат, α≠b≠с— все отрезки, отсекаемые на осях, разные.
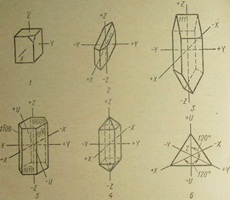
1 — триклинной; 2 — моноклинной; 3 — ромбической; 4 — тетрагональной; 5 — гексагональной; 6 — тригональной (показано сечение тригональной. призмы)
В тетрагональной сингонии ось Z проходит вдоль оси четвертого порядка, X и Y взаимно перпендикулярны друг другу и оси Z и располагаются вдоль осей второго порядка (рис. 4,4).
Если осей второго порядка нет, то оси X и У проводятся перпендикулярно к вертикальным плоскостям симметрии или параллельно ребрам кристалла.
Следует иметь в виду, что в тетрагональной сингонии при наличии 4-х осей второго порядка выбор положения осей X и Y не однозначен.
Так как их можно провести через любую пару осей, проходящих через середины противоположных ребер или через середины противоположных граней тетрагональной призмы.
В тетрагональной сингонии α=β=γ=90°, а=b≠с. Единичная грань отсекает равные отрезки на горизонтальных осях и пересекает вертикальную ось.
В гексагональной и тригональной сингониях применяют систему координат с четырьмя кристаллографическими осями: Помимо осей X, Y, Z используется дополнительная ось U.
Она проводится в одной плоскости с осями X и У под углом 120° к ним (рис. 4, 5, 6). Ось Z устанавливают соответственно .вдоль оси шестого или третьего порядков.
Остальные оси проводятся вдоль осей второго порядка, если их нет — перпендикулярно к плоскостям симметрии или параллельно трем ребрам кристалла.
Расположенным под углом 60° друг к другу и перпендикулярным к оси Z. Единичная грань отсекает на двух горизонтальных осях равные отрезки и пересекает ось Z.
Следует отметить, что единичная грань либо параллельна одной горизонтальной оси, либо отсекает на ней отрезок вдвое меньший, чем на двух других горизонтальных осях.
Для гексагональной и тригональной сингонии: α=β = 90°, γ = 120°, а=b≠с.
Для кристаллов тригональной сингонии возможна и другая установка, когда за координатные оси выбирают три ребра ромбоэдра или пирамиды. В этом случае α = β = γ=90°, a=b = c.
Символы граней в гексагональной и тригональной сингониях будут состоять из четырех индексов.
Индекс по оси X (первой кристаллографической оси) обозначается h, по У (второй кристаллографической оси) —Ʀ, по U (третьей кристаллографической оси) —i, по Z (четвертой кристаллографической оси)— l.
Таким образом, символ грани данных сингонии в общей форме выразится (hƦil).
Следует отметить, что индекс i может быть вычислен по формуле i= — (h+Ʀ), т. е. равен сумме индексов по первым двум осям с обратным знаком.
Статья на тему Кристаллографические символы


Добавить комментарий
Для отправки комментария вам необходимо авторизоваться.