РАЗВЕТВЛЕННАЯ ЦЕПЬ С АКТИВНЫМИ СОПРОТИВЛЕНИЯМИ И ИНДУКТИВНОСТЯМИ
I1 = U/z1 = U/√(r21 + x2L1)
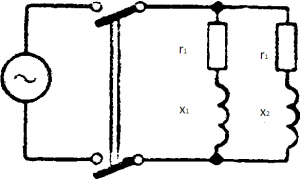
отстает по фазе от напряжения на угол, который можно определить через его tg φ1 = хL1/r1 Ток во второй параллельной ветви (рис. 5-25):
I2 = U/z2 = U/√(r22 + x2L2)
Рис. 5-25. Схема параллельного соединения двух катушек.
отстает по фазе от напряжения на угол, тангенс которого tg φ2 = хL2/r2
Для упрощения расчетов разветвленных цепей ток каждой ветви раскладывают на слагающие. Одна слагающая — активная (Iа) совпадает по фазе с напряжением. Другая слагающая — реактивная (Iр) сдвинута по фазе от напряжения на 90°.
Слагающие тока первой параллельной ветви:
Ia1 = I1 cos φ1 и Iр1 = I1 sin φ1.
При построении векторной диаграммы вектор активной слагающей тока откладывается по направлению вектора напряжения. Вектор реактивной индуктивной слагающей откладывается под углом 90° в направлении вращения часовой стрелки. Замыкающий вектор треугольника токов представляет собой вектор тока первой ветви
I1 = √(I2a1 + I2p1)
Для второй параллельной ветви Ia2 = cos φ2; Iр2 = I2 sinφ2; I = √(I2a2 + I2p2)
Сумма активных слагающих токов ветвей, совпадающих по фазе, равна активной слагающей общего тока
Ia = Ia1 + Ia2
Алгебраическая сумма реактивных слагающих токов ветвей, имеющих одну и ту же фазу, равна реактивной слагающей общего тока
Ip = Ip1 + Ip2
Общий ток, проходящий в неразветвленной части цепи,
I = √(I2a + I2p)
Этот ток сдвинут по фазе от напряжения на угол φ, который можно определить через
tgφ = Ip/Ia
Активная мощность цепи, равная сумме активных мощностей отдельных ветвей:
Р = Р1 + Р2 = UI1 cos φ + UI2 cos φ2 = UI cos φ.
Аналогично реактивная мощность цепи
Q = Q1 + Q2 = UI1 sin φ + UI2 sin φ = UI sin φ.
Полная мощность цепи
S = √(P2 + Q2)
Статья на тему Разветвленная цепь с сопротивлением

Добавить комментарий
Для отправки комментария вам необходимо авторизоваться.