ПОЛУЧЕНИЕ СИНУСОИДАЛЬНОЙ Э. Д. С.
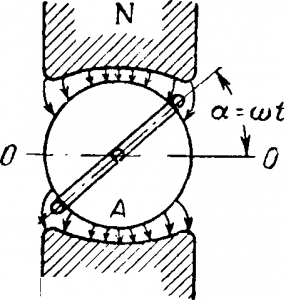
Полюсам придана такая форма, при которой воздушный зазор увеличивается от середины полюса к его краям и магнитная индукция В в зазоре вдоль окружности якоря у его поверхности изменяется по закону синуса, т. е.
В = Вм sin α,
где Вм — максимальная индукция под серединой полюса, а α — угол между нейтральной плоскостью 00‘, проходящей через ось якоря, и плоскостью, проведенной через ту же ось и произвольную точку на поверхности якоря.
Рис. 5-2. Схематическое устройство генератора переменного тока.
При вращении якоря с постоянной угловой скоростью ω = α/t в каждой активной стороне витка будет наводиться э.д. с.
е’= Blυ = Bмlυ sin α = Bмlυ sin ωt.
Активные стороны витка соединены последовательно, поэтому э. д. с, наведенная в витке,
е — 2e’ = 2Bмlυ sin ωt.
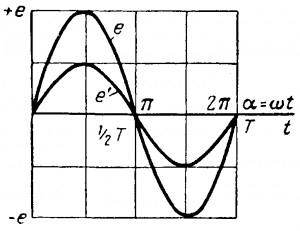
На рис. 5-3 приведены графики э. д. с. е = f (t) и e’ = f (t).
Если вместо одного витка на якоре будет катушка, имеющая ɯ витков, то э. д. с.
е = 2Bмɯυ sin ωt,
т. е. в ɯ раз больше.
Рис. 5-3. Графики переменных э. д. с.
При sin ωt = 1 э. д. с. будет иметь максимальное значение
Ем = 2Bмlɯυ
и, следовательно, наведенная в катушке якоря э. д. с.
е = Ем sin ωt.
Из написанного выражения следует, что в момент времени, принятый за начало отсчета t = 0, плоскость витка совпадает с нейтральной плоскостью, так как а = ωt = 0.
При постоянной скорости вращения якоря за один оборот его α = 2π происходит полный цикл изменения э. д. с, соответствующий одному периоду t = Т, поэтому угловая скорость вращения может быть выражена:
ω = α: t = 2π : T =2πf
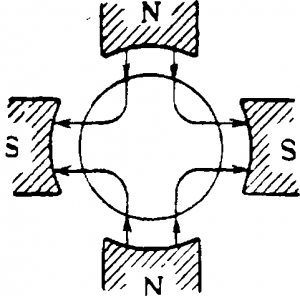
Кроме генераторов с одной парой полюсов, применяются генераторы с большим числом пар полюсов. У генератора с р парами полюсов (рис. 5-4) за один оборот его происходит р циклов изменения э. д. с, так как за один оборот каждый проводник р раз пройдет под северным и р раз — под южным полюсом.
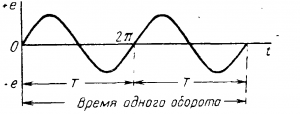
На рис. 5-5 приведен график е = f (t) за время одного оборота якоря генератора с двумя парами полюсов.
Для получения синусоидальной э.д.с. магнитная индукция у поверхности якоря многополюсного генератора с р парами полюсов должна изменяться по закону
Рис. 5-4. Генератор переменного тока с двумя парами полюсов.
В = Вм sin pα.
Произведение pα называется электрическим углом в отличие от геометрического угла α.
Отношение электрического угла ко времени pα/t = ω называется электрической угловой скоростью или угловой частотой. При t = Т будем иметь pα = 2π и, следовательно, для многополюсного генератора угловая частота
ω = 2π : T = 2πf
не зависит от числа пар полюсов генератора.
Рис. 5-5. График переменной э. д. с генератора с двумя парами полюсов.
Если якорь вращается со скоростью п, т. е. совершает п оборотов в минуту, то число циклов наведенной э. д. с. в минуту будет рп, а число циклов в секунду, т. е. частота,
f = pn : 60
а угловая частота
ω = 2πf = 2π(pn : 60)
Пример 5-1. Генератор, работающий совместно с паровой турбиной, имеет две пары полюсов (р = 2); Якорь его вращается со скоростью 1 500 об/мин. Определить частоту переменного тока
f = (pn) : 60 = (2 • 1500) : 60 = 50 гц.
Пример 5-2. Сколько пар полюсов должен иметь генератор, работающий совместно с гидротурбиной, имеющей номинальную скорость 250 об/мин, если генератор работает при частоте f = 50 гц.
p = (f • 60) : 60 = (50 • 60) : 250 = 12 пар.
Статья на тему Получение синусоидальной э. д. с.

Добавить комментарий
Для отправки комментария вам необходимо авторизоваться.