ВЫЧИСЛИТЕЛЬНЫЕ УСТРОЙСТВА
Успехи применения ЭВУ объясняются все возрастающим их быстродействием. Дело в том, что выполнение многих технических и народнохозяйственных задач требует решения сложных уравнений со многими неизвестными в короткий срок (прогнозы погоды, направление хода производственного процесса, вычисление траекторий спутников земли, ракет и др.). Решение этих уравнений, зачастую, возможно только путем разложения их на огромное число простейших операций, выполнение которых требует такого большого времени, что полученные результаты оказываются бесполезными. Только ЭВУ позволяют в этих случаях получать ответ своевременно. Если лет десять тому назад выполнение ЭВУ 2 000—4 000 математических операций в секунду считалось высоким показателем, то в настоящее время серийно изготовляемые ЭВУ производят десятки тысяч и более операций в секунду, а в некоторых ЭВУ оно достигает сотен тысяч операций в секунду.
СИСТЕМЫ ЭЛЕКТРОННЫХ ВЫЧИСЛИТЕЛЬНЫХ УСТРОЙСТВ
Вычислительные устройства можно разделить на две группы: вы числительные устройства непрерывного действия или аналоговые вычислительные устройства (АВУ) (называемые иногда модели-
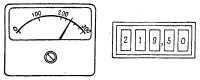
рующими) и цифровые вычислительные устройства (ЦВУ). На рис. 16-1 показано изображение одной и той же величины (напряжения), полученной двумя способами. В первом способе величина напряжения, например 219,5 в, измеряется стрелочным вольтметром. Измерение производится непрерывно и два ближайших значения измеряемой величины могут отличаться друг от друга на любую малую величину. Во втором способе величина напряжения выдается числом. В этом случае отличие одного значения меняющейся величины от другого зависит от числа
Рис. 16-1. Измерение величины приборами непрерывного и дискретного действия.
разрядов, предусмотренных в вычислительном устройстве. Так например, если для целых чисел предусмотрены три разряда, а для дробных — два, то в десятичной системе два ближайших значения величины будут отличаться друг от друга на одну сотую, т. е. 219,50; 219,51; 219,52. В АВУ точность решения ограничена точностью входящих в нее элементов (в данном случае вольтметра), а в ЦВУ она зависит только от количества разрядов в изображении числа и может быть очень большой. Скорость решения задачи в АВУ больше, чем в ЦВУ; они проще последних, но большей частью приспособлены для решения задач одного типа. Цифровые вычислительные устройства, сочетающие большую точность с высокой скоростью работы, универсальны, что дает возможность их применения в различных областях науки, техники, медицины и экономики.
АНАЛОГОВЫЕ ВЫЧИСЛИТЕЛЬНЫЕ УСТРОЙСТВА
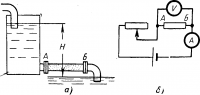
Рис. 16-2. Электрическая схема моделирующая гидравлическую установку.
В этих случаях пользуются методом математического моделирования, когда подбирается модель, действия которой описываются формулами, однотипными с формулами действия предполагаемого объекта.
Например, количество воды QB, фильтрующееся за время t через трубу АБ, заполненную песком (рис. 16-2, а) и имеющую гидравлическое сопротивление rг, при разности уровней воды Н равно
Qв = (H/rг)t
Но аналогичной формулой определяется количество электричества, проходящего через участок цепи АБ за время t (рис. 16-2, б):
Qэ = (Uав/rэ)t
Таким образом, явления, происходящие в этих установках, описываются одной формулой, но для производства испытания более удобна электрическая схема. Поэтому ее можно считать моделью гидравлической установки, показанной на рис. 16-2, a, хотя построена она на другой физической основе. В практике многие задачи математически определяются сложными уравнениями, решение которых требует огромного труда и времени. К этим задачам и применяется метод математического моделирования на электротехнической основе, как наиболее пригодной.
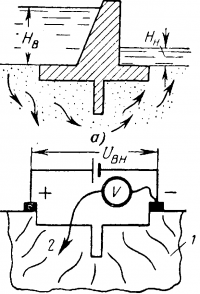
Рис 16-3. Определение напоров фильтрации воды в грунте под плотиной при помощи -электрической модели.
ВЫЧИСЛЕНИЯ В МОДЕЛИРУЮЩИХ УСТРОЙСТВАХ ПРИ ПОМОЩИ ПОТЕНЦИОМЕТРОВ
В автоматических устройствах и следящих системах сигналы, получаемые от датчиков, подвергаются различным преобразованиям сложению, вычитанию, умножению, делению, дифференцированию, интегрированию и решению уравнений, причем все это должно выполняться быстро и непрерывно. Такие операции выполняют вычислительные устройства непрерывного действия.
На рис, 16-4 показано устройство потенциометра, служащего для преобразования механической величины (угол поворота) в электрическую, выполнения операций умножения и деления, а в следящих системах для преобразования сигнала напряжения в угол поворота. На изолирующем каркасе 1 навит провод высокого удельного сопротивления.
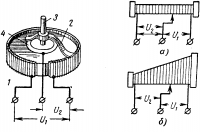
Щетка 2 при повороте оси 3 скользит по оголенной поверхности провода и по контактному кольцу 4.Таким образом, напряжение U1, подводимое к концам провода, делится щеткой 2 на U2 и U1 — U2.Каркас потенциометра показан развернутым на рис. 16-5, а. Такой потенциометр, у которого ширина каркаса неизменна, называется линейным, так как
U2 = U1(α/αм) = U1x
где α и αм — угол поворота щетки и его максимальное значение, ах — долевое значение угла α . Если х = const, то потенциометр служит блоком умножения на постоянный коэффициент, меньший единицы. Этот потенциометр служит также блоком умножения двух переменных величин U1 и если α и U1 меняются.
Очень часто в автоматических вычислительных устройствах потенциометр должен дать нелинейную зависимость между углом поворота и выходным напряжением. Тогда каркас должен иметь другую форму. Если rм и r — полное сопротивление потенциометра и часть его, то
U2/U1 = r/rм= f(x)
Изменение сопротивления, удельное сопротивление, изменение длины провода, се-
чение провода, ширина каркаса, изменение числа витков провода, полное число витков провода при перемещении щетки на расстояние ∆x. Тогда ширина каркаса
Рис. 16-6. Схема сложения напряжений при помощи потенциометров.
т. е. форма каркаса есть функция, пропорциональная производной заданной функции.
так как f‘(x) = 1; для f (х) = х2 каркас имеет треугольную форму, так как f’ (х) = 2х, что и показано на рис. 16-5, б и т. д. Такие потенциометры называются функциональными.
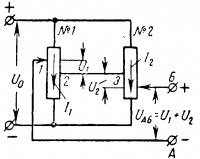
На рис.16-6 показано преобразование входных механических сигналов — перемещения движков потенциометров в выходные сигналы — напряжения и одновременное сложение этих напряжений на выходе схемы АБ. Потенциометры № 1 и № 2 присоединены к источнику энергии со стабилизированным напряжением U0, а средние точки их соединены накоротко. По потенциометрам проходят токи I1 и I2. В фазе с токами будут падения напряжения U1 = I1r1 и U2 = I2r2 где r1 и r2— части сопротивлений между движком и средними точками потенциометров. Если обойти контур между точками выхода А и Б в направлении А—1—2—3 —4—Б то легко понять, что Uаб = U1 + U2, и по сопротивлению какого-либо следующего каскада устройства rн пойдет ток от зажима Б к зажиму А. Когда движки стоят против средних точек, Uаб = 0.
На рис. -16-7 показана схема соединения потенциометров для получения разности напряжений Uаб = U1— U2, так как падения напряжения потенциометров при обходе контура А—1—2—3—4—Б вычитаются друг из друга.
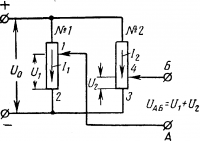
Рис. 16-7. Схема вычитания напряжений при помощи потенциометров.
НАЗНАЧЕНИЕ И ОБЩИЕ СВЕДЕНИЯ О ЦИФРОВЫХ ВЫЧИСЛИТЕЛЬНЫХ УСТРОЙСТВАХ (ЦВУ)
В некоторых случаях исследовать различные процессы в областях науки и техники при помощи моделей нецелесообразно. Кроме того, точность решения в АВУ, зависящая от точности входящих в них элементов, составляет несколько процентов. Однако при решении ряда вопросов допустимая погрешность должна быть в миллионы и миллиарды раз меньшей (расчет траекторий снарядов, ракет, спутников, планет). В ЦВУ точность решения может быть любой, так как она определяется только количеством разрядов чисел, на которое рассчитано устройство. Цифровые вычислительные устройства универсальны и могут применяться в любой области науки, техники, медицины, эконо-
мики и т. д. Эти устройства, кроме чисто вычислительных операций, могут решать логические задачи: определять знак произведения чисел, выделять части числа и составлять из них новые числа, переводить текст с одного языка на другой, решать шахматные этюды, подбирать библиографическую литературу и др.
Цифровые вычислительные устройства могут выполнять только те логические операции, которые выполняются человеком по установленным правилам и называются формальными видами умственного труда. Современные ЦВУ с применением электронной техники явились логическим продолжением механических вычислительных устройств.
ПРИНЦИП ПОСТРОЕНИЯ ЦВУ
Для решения всех задач одного типа (сложения двух многозначных чисел, извлечения квадратного корня и т. д.) можно составить точное предписание о выполнении, в определенном порядке, системы простейших операций, приводящих к результату. Такое предписание называется алгоритмом.
Сам термин происходит от имени средневекового узбекского математика Аль-Хорезми, который в IX веке дал правила для составления таких предписаний. Смысл предписаний в том, что они могут быть выполнены человеком без всякого понимания сути дела. От человека требуется машинальное, но точное выполнение простейших немногочисленных операций. А раз это так, то при современном состоянии электронной техники человека может заменить устройство, которое, с недостижимой для человека быстротой, сможет решить задачу, если это устройство снабдить алгоритмом, называемым в данном случае программой.
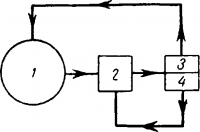
На рис. 16-8 показана структурная схема работы человека-вычислителя. В процессе работы вычислитель 1 для выполнения каждого действия пользуется программой 3, записанной при помощи цифр, букв, знаков алгебраических операций и др. По этим сведениям он производит вычисления на бумаге, на счетах или арифмометре, т. е. вводит в действие имеющееся него арифметическое устройство 2. После вычислений, он их записывает в определенную графу (ячейку) на бумаге, которая служит запоминающим устройством 4, способным длительно хранить полученные результаты. То, что не нужно хранить длительно человек держит в памяти для следующей операции. Выполнив первый пункт программы, вычислитель берет требуемые программой результаты из запоминающего устройства 4 и выполняет второй пункт программы и т. д. Таким образом, пункт за пунктом выполняется вся программа вычисления. На основании сказанного, очевидно, и для ЦВУ нужно иметь структурную схему, подобную показанной на рис. 16-8.
Структурная схема современного ЦВУ показана на рис. 16-9. На этой схеме устройство управления, очевидно, должно выполнять функции человека-вычислителя. Запоминающее устройство обычно состоит из двух отдельных блоков: внешнего запоминающего устройства, имитирующего записи вычислителя на бумаге, справочники, таблицы и др., и оперативного запоминающего устройства, хранящего только те сведения, которые быстро и непрерывно используются при вычислениях, и длительно храниться не должны. Арифметическое устройство заменяет все средства вычисления, которыми пользовался вычислитель: бумага, счеты, арифмометр, клавишная механическая машина и др. По видимому, ЦВУ будет только тогда быстродействующим (тысячи и десятки тысяч операций в секунду), когда с такой же скоростью будут работать все блоки устройства, К сожалению, этому условию еще не удовлетворяют блоки ввода программы и вывода результатов. Описание устройства отдельных блоков будет дано ниже.
ВЗАИМОДЕЙСТВИЕ ОТДЕЛЬНЫХ БЛОКОВ ЦВУ
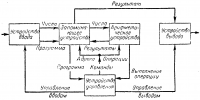
Управление ЦВУ производится при помощи электрических импульсов напряжения или тока, которые усиливаются, формируются для придания им прямоугольной формы и в определенных условных комбинациях могут представлять числа. Эти импульсы формируются в устройстве управления и при помощи их производится выборка чисел и команд из запоминающего устройства. В соответствии с адресом числа передаются из запоминающего устройства в арифметическое, где над ними производится вычислительная операция указанная кодом команды. Результат вычислений передается обратно в запоминающее устройство, по адресу, указанному командой (рис. 16-9). После окончания одной операции устройство управления получает из арифметического устройства ответ о выполнении операции и переходит к следующему пункту программы.
Статья на тему Вычислительные устройства

Добавить комментарий
Для отправки комментария вам необходимо авторизоваться.