ВРАЩАЮЩИЙ МОМЕНТ ЭЛЕКТРОДВИГАТЕЛЯ
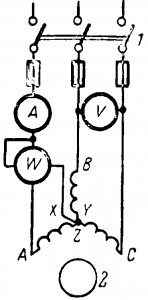
М ≡ ФI2 cos Ψ2.
Следовательно, момент пропорционален потоку и активной слагающей тока ротора I2 cos Ψ2, так как только активная слагающая тока определяет мощность, а значит и момент.
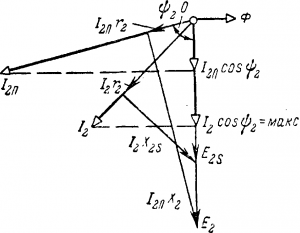
На рис. 10-20 представлена схема включения короткозамкнутого двигателя. Если пустить двигатель, включив рубильник 1, то в первый момент пуска, когда п2 = 0, a s = 1, наведенная в роторе 2 э. д. с. Е2 и пусковой ток I2п максимальны. Однако, пусковой момент Мп не будет максимальным, а в 2—2,5 раза меньше максимального. Векторная диаграмма для цепи ротора (рис. 10-21), построенная подобно изображенной на рис. 9-9, показывает причину этого.
Рис 10-20. Схема включения короткозамкнутого асинхронного двигателя.
Обычно в роторе х2 во много раз больше r2 и угол Ψ2, на который ток I2п отстает от э. д. с. Е2 велик. Поэтому активная слагающая тока I2п cos Ψ2, а значит и пусковой момент Мп малы. В современных асинхронных двигателях Мп/Мп = 1 — 1,5, хотя I2п/ Iн≈ 4,5—6,5.
Это же явление по другому объясняется на рис. 10-19 и 10-22.
Рис. 10-21. Векторная диаграмма в цепи ротора.
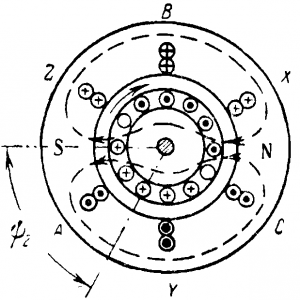
При описании принципа работы двигателя (рис. 10-19) было предположено, что ток I2 совпадает по фазе с э. д. с. Е2, т. е. что он активный (Ψ2 = 0). На рис. 10-22 представлен момент пуска, когда направление э. д. с. в проводах ротора соответствует обозначенному на рис. 10-19, а ток показан отстающим от э. д. с. на угол Ψ2. Тогда шесть проводов ротора (три под полюсом N и три под полюсом S) создают усилия, действующие в направлении вращения потока, а два провода вызывают противодействующие усилия. В результате этого вращающий момент будет тем меньше, чем больше сдвиг фаз между током I2 и э. д. с. E2.
Рис. 10-22. Ток в роторе двигателя в момент пуска.
По мере увеличения скорости вращения ротора реактивное сопротивление обмотки ротора x2s = x2s уменьшается, а вместе с этим уменьшается угол Ψ2, так как сопротивление r2 ≈ const. Наступает такое положение (рис 10-21), когда при некотором скольжении sм ≈ 0,1—0,15 реактивное сопротивление x2s становится равным активному r2, угол Ψ — 45° и э. д. с. E2s уравновешивает два равных падения напряжения I2r2 и I2x2s.В это время активная слагающая тока I2 cos Ψ2 и вращающий момент Мм становятся максимальными, несмотря на некоторое уменьшение тока I2.
Обычно Мм/Мм = 1,8—2,5 и называется способностью к перегрузкe.
При дальнейшем разгоне ротора x2s становится значительно меньшим, чем r2, им можно пренебречь и считать ток ротора активным (I2 ≈ I2 cos Ψ2). Так как E2s = E2s тоже продолжает уменьшаться, то вместе с током I2 уменьшается и вращающий момент.
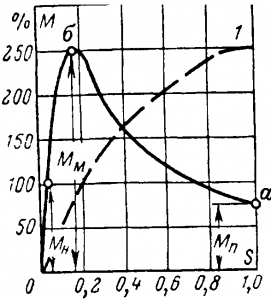
Максимальная скоростьn вращения будет при холостом ходе двигателя и тогда n2 ≈ n1 , a s ≈ 0. Зависимость вращающего момента от скольжения М = f (s) представлена на рис. 10-23.
Рис. 10-23. Зависимость вращающего момента двигателя от скольжения.
Нормальная работа двигателя возможна только на участке кривой при скольжениях s от нуля до sм, так как в этом случае при увеличении тормозного момента и значит s вращающий момент возрастает. На участке от s = sм до s = 1 работа двигателя неустойчива. Номинальный момент Мн соответствует обычно номинальному скольжению sн = 1—6%.
Поток Ф пропорционален напряжению U1, подводимому к трансформатору. Сказанное остается в силе и для асинхронного двигателя. Так как М ≡ ФI2 cos Ψ2, то можно написать, что
I2 cos Ψ2 ≡ E2s ≡ Ф ≡ U1
Отсюда можно сделать очень важный для асинхронных двигателей вывод
M ≡ U1U1 ≡U21
т. е. вращающий момент пропорционален квадрату подведенного к статору напряжения. Таким образом, падение напряжения в сети, например до 0,9 U1н, вызовет уменьшение момента до 0,9 • 0,9 Мн = 0,81 Мни нагруженный двигатель может остановиться. Указанным обстоятельством и объясняется, частично, нормирование падения напряжения в распределительных сетях, питающих асинхронные двигатели.
В практике потребителя часто интересует механическая характеристика двигателя
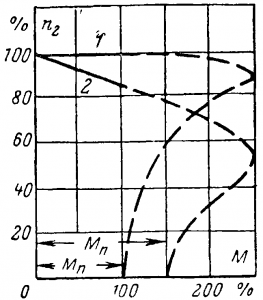
п2 = f (М) при U1 = const и f1 = const. Для удобства пользования по осям откладывают (n2/n1)100% и (М/Мн)100%.
Рис. 10-24. Механическая характеристика двигателя.
Эта характеристика получается простым перестроением рис, 10-23 и показана на рис. 10-24, где рабочая часть обозначена сплошной линией. Кривая 1 для двигателей нормального исполнения показывает, что асинхронный двигатель обладает жесткой характеристикой скорости, подобно двигателю постоянного тока параллельного возбуждения. Асинхронный двигатель с фазным ротором для регулирования скорости вращения, например для крановых и подъемных устройств, имеет более мягкую характеристику (кривая 2).
РАБОЧИЙ ПРОЦЕСС АСИНХРОННОГО ДВИГАТЕЛЯ
Трехфазный ток I1протекая в трехфазной обмотке статора, создает н. F1, вращающуюся со скоростью п1= (f1•60)/p (рис. 10-4, 10-5). Трехфазный ток ротора I2 создает в трехфазной обмотке ротора н. с. F2вращающуюся вокруг ротора со скоростью п3 = (f1•60)/p . Сам ротор вращается в сто-
рону н. с. со скоростью n2. Тогда скорость вращения н. с F2 относительно статора равна:
п2 + п3 = п2 +(f2 • 60)/p = n2 + (f1s • 60)/p = n2 + n1s = n2 + n1((n1 — n2)/n1) = n1
Таким образом, обе н. с. F1 и F2 вращаются с одной скоростью n1, друг относительно друга неподвижны и создают сообща вращающийся магнитный поток Ф. Следовательно, все приведенное на рис. 9-8 и 9-9 справедливо и для асинхронного двигателя.
Следует отметить, что благодаря воздушному зазору между ротором и статором ток холостого хода (рис. 9-7) двигателя очень велик (20—40)% I1Н. Поэтому для улучшения cos φ1 сети двигатель необходимо нагружать полностью.
Статья на тему Вращающий момент электродвигателя

Добавить комментарий
Для отправки комментария вам необходимо авторизоваться.