Яркость — это характеристика интенсивности или уровня зрительного ощущения. Она зависит от мощности излучения, действующего на световоспринимающие элементы глаза, и от их светочувствительности.
При этом светочувствительность в свою очередь зависит от спектрального состава излучения, а также и от степени адаптации глаза.
В связи с адаптацией глаз может оценивать абсолютную величину яркости только очень приближенно, хотя он весьма чувствителен к разнице яркостей, особенно при одновременном наблюдении.
Что такое яркость
Основными, оцениваемыми субъективно характеристиками зрительного ощущения являются: цвет и яркость.
Цвет — качественная характеристика зрительного ощущения, она зависит главным образом от спектрального состава (длины волны) излучения и светочувствительности глаза.
Можно отметить некоторую аналогию между характеристиками слухового (высота и тембр, громкость) и зрительного (цвет, яркость) ощущений, а также их связью со спектральным составом и мощностью звуковой или световой волны. Эта аналогия, однако, не распространяется на системы звуковых и световых измерений.
Исторически (это значение она сохраняет и в наши дни) система световых измерений была построена, исходя из требований практики, применительно в основном к оценке источников света, хотя в какой-то степени в ней учтены также и условия восприятия света глазом.
В частности, определенные величины в этой системе имеют прямую связь с визуальной яркостью.
Система является объективной, в основу ее положен эталонный источник света, воспроизводящий основную единицу измерения — свечу. Эталон дает излучение определенного спектрального состава, которое приближается к белому свету.
К такому излучению, строго говоря, и относится вся система. Практически она распространяется на измерения в области как дневного света, так и белого света от различных источников искусственного освещения.
Исходной величиной в системе световых измерений является световой поток. Это величина, характеризующая лучистый поток с точки зрения его способности вызывать (в определенных пределах длины волны) зрительное ощущение.
Световой поток
Световым потоком называется лучистый поток, оцениваемый по зрительному ощущению, которое оно вызывает в среднем по чувствительности человеческом глазу.
Можно отметить, что в этом определении еще не устанавливается прямой связи между световым потоком и характеристиками зрительного ощущения. Единицей измерения светового потока является люмен.
Для монохроматического излучения световой поток Ф численно связан с лучистым потоком Фэ через коэффициент пропорциональности μ, учитывающий светочувствительность глаза и называемый коэффициентом видности:
Ф = μФэ.
Для монохроматического излучения коэффициент видности зависит от длины волны соответственно изменению относительной спектральной чувствительности глаза.
Максимальная величина коэффициента видности для желто-зеленого света λ = 555 ммк), к которому глаз наиболее чувствителен, определена как μт = 683 лм/вт.
Для сложного излучения световой поток находится по распределению энергии в спектре. Для каждого характерного интервала длин волн лучистый поток умножается на соответствующий коэффициент видности; результаты суммируются.
При приближенных расчетах для белого света учитывается только лучистый поток, приходящийся на интервал длин волн, близких к максимальной чувствительности глаза.
Сила света
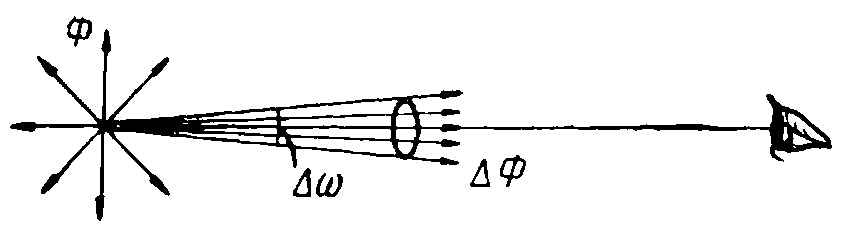
I = ∆Ф/∆ω
Силу света можно определить так же, как световой поток, приходящийся на единичный телесный угол, ориентированный в определенном направлении.
Практическое значение силы света связано с тем, что из полного светового потока, распространяющегося от источника по всем направлениям, полезной в большинстве случаев является только та его часть, которая распространяется в сторону наблюдаемых предметов и в конце концов попадая в глаз, вызывает зрительное ощущение.
Например, при наблюдении точечного источника света в глаз попадает только малая часть излучаемого им светового потока, которая распространяется в пределах телесного угла ω при вершине конуса, основанием которого является площадь зрачка, а вершиной источник света.
Для точечного источника, равномерно излучающего по всем направлениям световой поток Ф, полный телесный угол равен 4π рад, следовательно, сила света по любому направлению:
I = Ф/4π .
Для плоского источника конечных размеров, излучающего полный световой поток Ф, сила света I0 в направлении, перпендикулярном излучающей поверхности (рис. 3, а) I0=Ф/π , а сила света I в каком-либо другом направлении равняется силе света I0, умноженной на косинус угла а между перпендикуляром к поверхности и рассматриваемым направлением (закон Ламберта):
I = I cos α = Ф/π cos α.
Источники, удовлетворяющие этому условию, называются ламбертовыми, или косинусными излучателями. Таким излучателем является абсолютно черное тело, приближается к нему также Солнце.
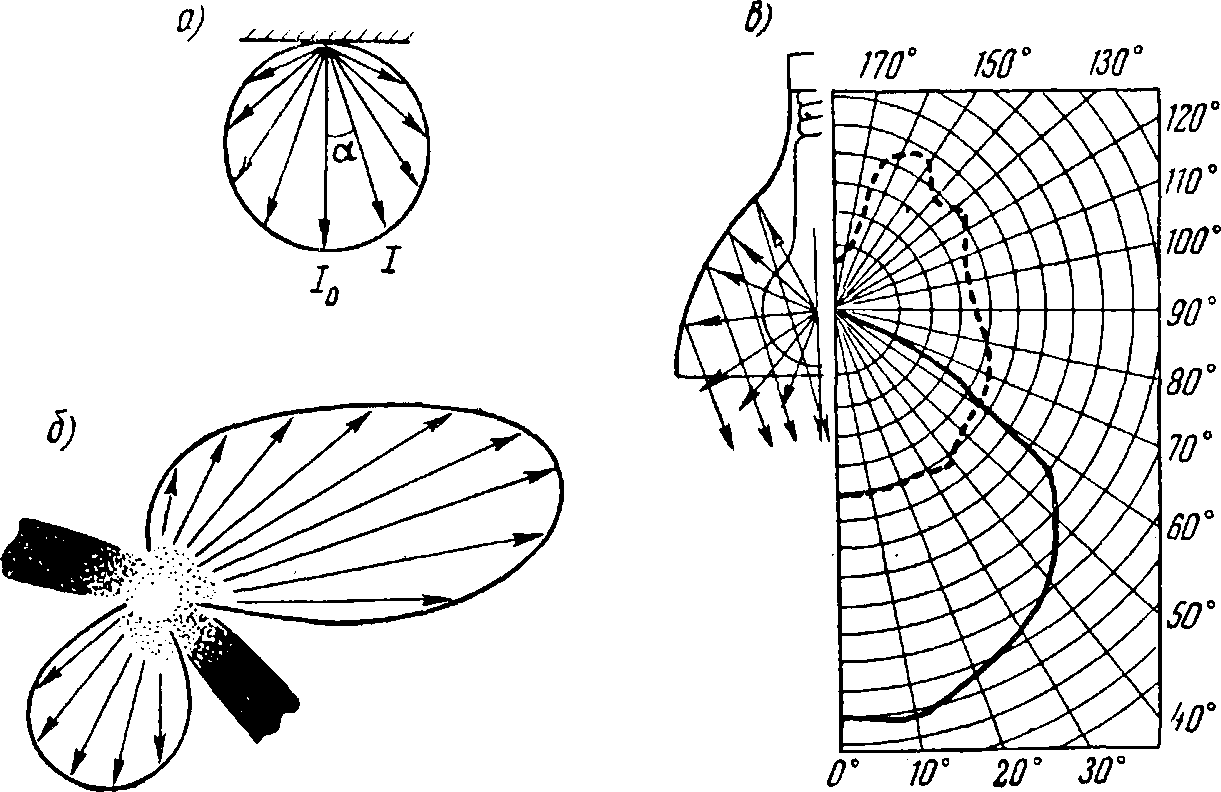
Распределение силы света источника по различным направлениям имеет большое практическое значение. Для характеристики его строят специальные диаграммы. От точки О (рис. 3, б), совмещенной с центром источника, в определенной плоскости по радиусам откладываются величины силы света по различным направлениям.
Концы векторов соединяются кривой, которая и дает картину распределения силы света источника в данной плоскости. На рис. 3, а приведена диаграмма для плоского источника небольших размеров (ламбертов излучатель), на рис. 3, б — для электрической дуги.
На рис. 3, в приведены диаграммы для электролампы (пунктиром) и для той же лампы, снабженной отражательным рефлектором (сплошным). Как видно из рисунка, применение рефлектора позволяет увеличить силу света лампы в желаемых направлениях больше, чем в два раза.
Величина М, равная отношению полного светового потока Ф, равномерно излучаемого по всем направлениям с площади 5 источника (рис. 4, а) к величине этой площади, называется светимостью (или светностью) данной поверхности:
М = Ф/S
Светимость может быть определена как полный световой поток, излучаемый с единицы площади источника.

Например, законно говорить о светимости ясного неба и т. п.
Величина Е, равная отношению полного светового потока Ф, равномерно падающего по всем направлениям на площадь S освещаемой поверхности (рис. 4, б) к величине этой площади, называется освещенностью данной поверхности:
Е = Ф/S
Освещенность можно определить так же, как полный световой поток, падающий на единицу освещенной площади.
Первый закон освещенности
Сила света и освещенность находятся между собой в определенном соотношении. Если источник света имеет размеры значительно меньшие, чем расстояние его от освещаемой поверхности, то он может приближенно считаться точечным.
Допустим, что он дает по всем направлениям силу света I, тогда полный световой поток от него Ф = 4πI. Проведем вокруг источника света сферу радиусом R (рис. 4, в). Поверхность сферы будет S = 4πR2 и освещенность ее:
E = Ф/S = 4πI/4πR2 = I/R2
т. е. освещенность поверхности, перпендикулярной направлению лучей, прямо пропорциональна силе света и обратно пропорциональна квадрату расстояния до источника (I закон освещенности).
Второй закон освещенности
Если лучи падают на поверхность под некоторым углом а, то освещенность Е поверхности будет меньше, чем освещенность Е0 при перпендикулярном падении лучей.
Пусть на поверхность S падает под углом α равномерный световой поток Ф; спроектируем поверхность S на плоскость, перпендикулярную направлению падения лучей. Получим поверхность S0 = S cos α.
Освещенность поверхности S : Е = Ф/S ; освещенность поверхности S0 : E0 = Ф/S0 = Ф/S cos α . Отношение освещенностей:
E/E0 = (Ф/S) : (Ф/S cosα) = cos α, откуда Е = E0 cos α.
Освещенность поверхности световым потоком, падающим под некоторым углом, прямо пропорциональна косинусу угла падения лучей (II закон освещенности).
Изменение угла падения солнечных лучей по отношению к поверхности земли вызывает, например, разницу в климатических поясах земного шара (жаркий на экваторе, где лучи Солнца падают перпендикулярно, и холодный у полюсов.
Где лучи Солнца падают почти касательно), а также и разницу в температурах в различное время дня в одном и том же месте земной поверхности: утром и вечером более прохладную, когда лучи падают под наибольшим углом, и в полдень — наиболее жаркую, когда лучи падают под наименьшим углом.
Пример определения яркости
При данных степени адаптации глаза (влияние адаптации глаза в системе световых измерений не учитывается) и спектральном составе света визуальная яркость прямо пропорциональна энергии излучения.
Поглощаемой каждым светочувствительным элементом сетчатки в единицу времени, или, пренебрегая отражением излучения от сетчатки, — падающему на каждый светочувствительный элемент световому потоку.
Принимая площадь сетчатки, занимаемую каждым элементом, за единицу, можно сказать, что визуальная яркость прямо пропорциональна освещенности сетчатой оболочки глаза.
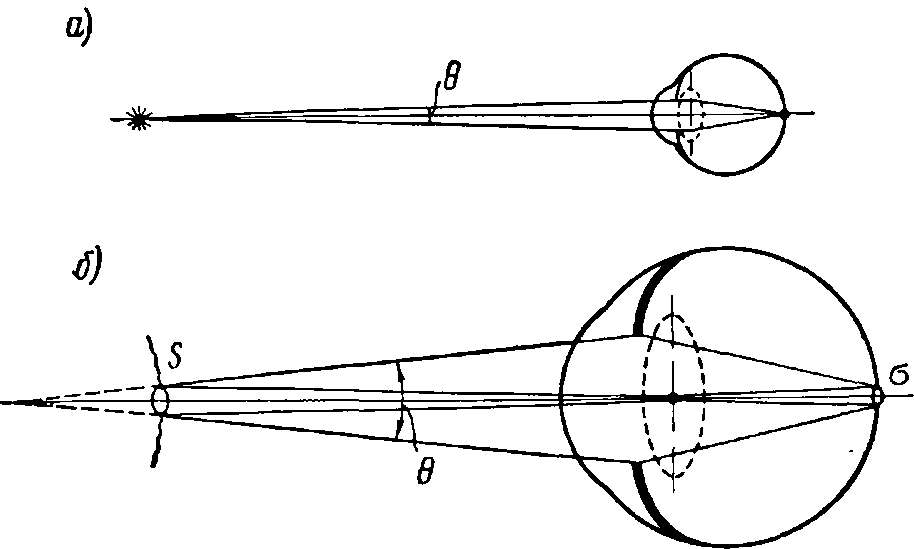
При наблюдении точечного источника света можно считать, что его изображение падает на один светочувствительный элемент сетчатки, тогда освещенность сетчатки численно равна попадающему в глаз световому потоку φ0.
Этот поток равен произведению силы света I источника на телесный угол 0, основанием которого служит площадь зрачка глаза (рис 5, а):
φ0 = ϴI.
Таким образом, в этом случае освещенность сетчатки, а следовательно, и визуальная яркость будут прямо пропорциональны силе света I источника , а также (вследствие изменения при этом угла 0) обратно пропорциональны квадрату расстояния от источника до глаза.
В случае протяженного источника света, например, если глаз наблюдает площадку (для простоты рассуждений небольшой площади, круглой формы и расположенную перпендикулярно направлению к центру глаза).
Скоторой равномерно по всем направлениям излучается световой поток Ф, то в глаз через зрачок попадает только световой поток φS, излучаемый с этой площадки внутри телесного угла б, ориентированного в направлении глаза.
Поток φS распределяется на площадке о сетчатой оболочки, которая является изображением площадки S источника. При этом на площадь, занимаемую одним светочувствительным элементом, приходится световой поток Еσ = φS/ σ. В данном случае Еσ есть освещенность сетчатки, которой пропорциональна визуальная яркость.
Площадь о изображения на сетчатке (при данном расстоянии от источника до глаза) прямо пропорциональна площади 5 источника:
σ = k1S,
а поток φS , попадающий в глаз (при неизменной площади зрачка), прямо пропорционален силе света I источника в направлении глаза:
φS = k2I.
Подставляя эти соотношения в предыдущую формулу, получим:
Eσ = φS /σ = k2I/k1S = k(I/S) = kB,
где k некоторый коэффициент пропорциональности, В — величина, называемая фотометрической яркостью светящейся поверхности.
Таким образом, при наблюдении протяженной светящейся поверхности визуальная яркость прямо пропорциональна ее фотометрической яркости.
Фотометрическая яркость
Фотометрическая яркость (а следовательно, и визуальная яркость) не зависит от расстояния между поверхностью и глазом, так как при его изменении и световой поток, попадающий в глаз, и площадь изображения на сетчатке изменяются в одинаковом соотношении.
Например, два белых экрана одинаково освещенных,- но находящихся на различных расстояниях от глаза, будут наблюдаться одинаково яркими.
Если силу света I выразить через световой поток Ф, то рассмотренное выше соотношение примет вид:
Eσ = k(I/S) = k(∆Ф/∆ωS),
откуда В = ∆Ф/∆ωS
Фотометрическую яркость светящейся поверхности можно определить как:
- Величину, измеряемую силой света, которая излучается с единицы площади поверхности в направлении глаза;
- Величину, измеряемую световым потоком, который излучается с единицы площади поверхности внутри единичного телесного угла, ориентированного по направлению к глазу.
Если светящаяся поверхность расположена под некоторым углом β (β есть угол между направлением видения глаза и перпендикуляром к поверхности), то в предыдущее соотношение войдет проекция светящейся поверхности на плоскость, перпендикулярную направлению видения глаза или, другими словами, «видимая глазом величина светящейся поверхности». При этом формула для фотометрической яркости примет вид:
В = I/Scosβ = ∆Ф/∆ωS cos β
Для самосветящейся плоской поверхности, перпендикулярной направлению видения, фотометрическая яркость В находится в прямом соотношении со светимостью М. В этом случае сила света I 0 и поток Ф, излучаемый поверхностью, связаны соотношением I0 = Ф/π. Подставляя это в формулу для яркости, получим:
В = I0/S = Ф/πS = M/π.
Аналогично светимости и фотометрическая яркость характеризует не только излучающие, но и освещенные, диффузно отражающие свет поверхности.
Для диффузно отражающей свет плоской перпендикулярной направлению видения поверхности фотометрическая яркость В находится в прямом соотношении с освещенностью Е. Действительно, светимость М диффузно отражающей свет поверхности:
М = rЕ,
где r — коэффициент отражения, тогда яркость
B = M/π = rE/π = (r/π)E.
Фотометрическая яркость, которая является объективной величиной, характеризующей как самосветящиеся, так и диффузно отражающие свет освещенные поверхности, входит в систему световых величин и при этом часто называется просто яркостью.
Яркость глаз
На практике, когда глазом наблюдаются и оцениваются освещенные поверхности, а также экраны и поля зрения оптических приборов или изображения, образованные с помощью оптических систем, следует говорить именно об их яркости (а не освещенности, как иногда ошибочно делают), так как только яркость может непосредственно оцениваться глазом. Хотя численно яркость и освещенность, как показано выше, находятся в прямом соотношении.
Пропорциональность визуальной и фотометрической яркостей установлена без учета адаптации глаза и показывает только соответствие этих величин.
Сопоставляя эти величины в условиях их изменения, следует иметь в виду, что в связи с адаптацией глаза изменение фотометрической яркости будет вызывать значительно меньшее изменение визуальной яркости.
В соответствии с законом Вебера—Фехнера изменение визуальной яркости пропорционально логарифму от изменения фотометрической яркости.
Реферат на тему яркость


Добавить комментарий
Для отправки комментария вам необходимо авторизоваться.